
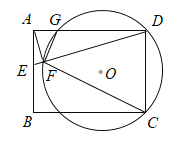
【题目】如图,在矩形ABCD中,E 是AB 上的一点,连接DE,过点A作AF⊥DE,垂直为F.圆O经过点C ,D ,F,且与AD相交于点G.
(1)求证,△AFG∽△DFC;
(2)若AB=3,BC=5,AE=1,求圆O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)欲证明△AFG∽△DFC,只要证明∠FAG=∠FDC,∠AGF=∠FCD;
(2)首先证明CG是直径且△EDA∽△ADF,结合△AFG∽△DFC,利用相似三角形的性质求出AG,得到DG,再利用勾股定理求出CG即可解决问题.
(1)证明:在矩形ABCD中,∠ADC=90°,
∴∠CDF+∠ADF=90°,
∵AF⊥DE,
∴∠AFD=90°,
∴∠DAF+∠ADF=90°,
∴∠DAF=∠CDF,
∵四边形GFCD是⊙O的内接四边形,
∴∠FCD+∠DGF=180°,
∵∠FGA+∠DGF=180°,
∴∠FGA=∠FCD,
∴△AFG∽△DFC.
(2)解:如图,连接CG.
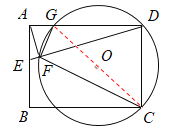
∵∠ADC=90°,
∴CD为⊙O的直径,
∵∠EAD=∠AFD=90°,∠EDA=∠ADF,
∴△EDA∽△ADF,
∴![]() ,即
,即![]() ,
,
∵△AFG∽△DFC,
∴![]() ,
,
∴![]() ,
,
在矩形ABCD中,DA=BC=5,DC=AB=3
∴![]()
∴DG=AD-AG=5-![]() =
=![]() ,
,
在Rt△CDG中,![]()
∵CG是⊙O的直径,
∴⊙O的半径为![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】(问题情境)定义:如图1,点E在四边形ABCD的边CD上,若AE、BE将四边形ABCD分割成三个相似的三角形,则称点E为该四边形的相似点.

(1)若相似点在四边形ABCD的边CD上, 且AE、BE将四边形ABCD分割成三个正三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(2)若相似点在四边形ABCD的边CD上,且AE、BE将四边形ABCD分割成三个全等的等腰直角三角形,则四边形ABCD的四边形之比(按边长从小到大排序)为_______.
(3)(探索研究)
如图2,点E为四边形ABCD边上的相似点,且AE、BE将四边形ABCD分割成三个全等的三角形,已知∠ABC=90°,AD=AB=BC=2,求边CD的长.
(4)(问题解决)
如图3,在四边形ABCD中,AB∥CD,点E为四边形ABCD的边CD上的相似点,且AD=a,AB=b,BC=c(其中a≠c),此时边CD的长为多少?请用含a、b、c的代数式直接写出所有可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校1000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 | 0.05 |
| 20 | 0.10 |
| 30 |
|
|
| 0.30 |
| 80 | 0.40 |
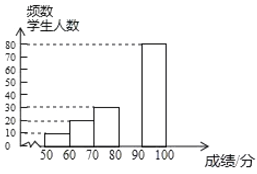
请根据所给的信息,解答下列问题:
(1)![]() _____,
_____,![]() _____;
_____;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在______分数段;
(4)若成绩在90分以上(包括90分)的为优等,则该校参加这次比赛的1000名学生中成绩优等的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
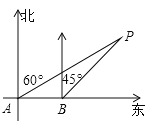
【题目】如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
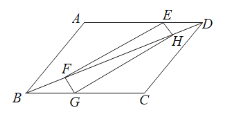
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD ,BC上,顶点F,H在菱形ABCD的对角线BD上,若AB=6,∠A=120°,且DE=2,则FH=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
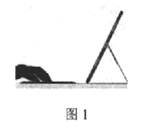
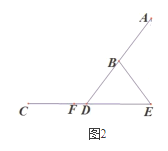
【题目】图1是一台用保护套套好的带键盘的平板电脑实物图,图2是它的示意图,忽略平板电脑的厚度,支架BE分别固定在平板电脑AD背面中点B处,桌面E处,EB可以绕点E转动,当点D在线段EF上滑动时,可调节平板电脑AD的倾斜角![]() ,经测量,
,经测量,![]() ,
,![]() ,支架
,支架![]() .
.
(1)连接AE,求证:![]() ;
;
(2)当![]() 时,求A,E两点间的距离;
时,求A,E两点间的距离;
(3)当点D滑到距离F点1cm处时,视觉效果最好,求此时倾斜角![]() 的度数.
的度数.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,结果保留一位小数)
,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() .
.
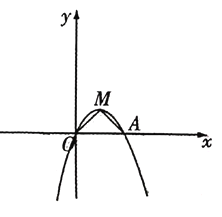
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)已知点![]() 的坐标为
的坐标为![]() ,将抛物线
,将抛物线![]() 向上平移得到抛物线
向上平移得到抛物线![]() ,抛物线
,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() (点
(点![]() 在点
在点![]() 的左侧),如果
的左侧),如果![]() 与
与![]() 相似,求所有符合条件的抛物线
相似,求所有符合条件的抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,tan∠A=![]() ,M,N分别在AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,
,M,N分别在AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,![]() 的值为_____.
的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
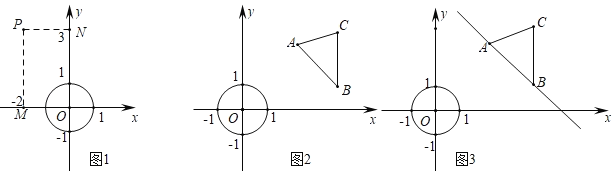
【题目】在平面直角坐标系xOy,对于点P(xp,yp)和图形G,设Q(xQ,yQ)是图形G上任意一点,|xp﹣xQ|的最小值叫点P和图形G的“水平距离”,|yp﹣yQ|的最小值叫点P和图形G的“竖直距离”,点P和图形G的“水平距离”与“竖直距离”的最大值叫做点P和图形G的“绝对距离”
例如:点P(﹣2,3)和半径为1的⊙O,因为⊙O上任一点Q(xQ,yQ)满足﹣1≤xQ≤1,﹣1≤yQ≤1,点P和⊙O的“水平距离”为|﹣2﹣xQ|的最小值,即|﹣2﹣(﹣1)|=1,点P和⊙O的“竖直距离”为|3﹣yQ|的最小值即|3﹣1|=2,因为2>1,所以点P和⊙O的“绝对距离”为2.
已知⊙O半径为1,A(2,![]() ),B(4,1),C(4,3)
),B(4,1),C(4,3)
(1)①直接写出点A和⊙O的“绝对距离”
②已知D是△ABC边上一个动点,当点D与⊙O的“绝对距离”为2时,写出一个满足条件的点D的坐标;
(2)已知E是△ABC边一个动点,直接写出点E与⊙O的“绝对距离”的最小值及相应的点E的坐标
(3)已知P是⊙O上一个动点,△ABC沿直线AB平移过程中,直接写出点P与△ABC的“绝对距离”的最小值及相应的点P和点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com