
����Ŀ����ͼ����֪AB����O��ֱ����BC����O�����ڵ�B��CD����O�����ڵ�D������AD��
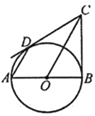
(1)��֤��AD��OC��
(2)С����С�����������Ŀ��ʱ����CDA����AOC֮��Ĺ�ϵ������̽����
С��˵����CDA+��AOC��ֵ��һ���̶���ֵ��
С��˵����CDA+��AOC��ֵ����A�����ı仯���仯.
����CDA+��AOC��ֵΪy����A����Ϊx������Ϊ����֮��˭˵������ȷ��?������ΪС��˵����ȷ�������������̶�ֵ��������ΪС��˵����ȷ���������y��x֮��Ĺ�ϵ��
���𰸡�(1)֤����������(2)С��˵�Ķԣ���CDA+��AOC��ֵ��һ���̶���ֵ��270��.
��������
��1������OD�������������ʵá�ODC=��OBC=90������ȫ���������ж�HL��Rt��ODC��Rt��OBC������ȫ�����������ʵá�DOC=��BOC�������������ڽǺͶ�����ƽ�ǵá�ODA+��OAD=��DOC+��BOC���Ӷ��ɵá�ODA=��DOC����ƽ�����ж����ɵ�֤.
��2��С��˵�Ķԣ���CDA+��AOC��ֵ��һ���̶���ֵ���������£���������ɵ�90��+x+��AOC=y����x+��AOC=y-90������ƽ�������ʵá�OAD+��AOC=180������x+��AOC=180������ʽ�����ɵ�90��+180��=y=270��.
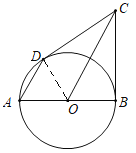
�⣺(1)����OD����ͼ��
 ��
��
�� BC���O�����ڵ�B��CD���O�����ڵ�D��
���ODC=��OBC=90����
��OD=OB��OC=OC��
��Rt��ODC��Rt��OBC(HL)��
���DOC=��BOC��
��OA=OD��
���ODA=��OAD��
�ߡ�AOD+��ODA+��OAD=180������AOD+��DOC+��BOC=180����
���ODA+��OAD=��DOC+��BOC��
���ODA=��DOC��
��AD��CO.
(2)С��˵�Ķԣ���CDA+��AOC��ֵ��һ���̶���ֵ���������£�
�ߡ�CDA+��AOC=y����A=x��
���ODA=��OAD=x����ODC+��ODA+��AOC=y��
�ߡ�ODC=90����
��90��+x+��AOC=y��
��x+��AOC=y-90����
��AD��CO��
���OAD+��AOC=180����
��x+��AOC=180����
��90��+180��=y��
��y=270����
��С��˵�Ķԣ���CDA+��AOC��ֵ��һ���̶���ֵ.


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ǰ���ͼ��ʾ��������һ�����̶���AOB������ACD���Ź�����A��˳ʱ�뷽����ת����(0������180)������̽��������ACD��һ�����AOB��һ��ƽ��ʱ����Ӧ����ת�����Ķ���_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABCD�У�AB��3��BC��5����BAC��90����E��F�ֱ���AB��BC�ϵĶ��㣬EF��BC����BEF����PEF����ֱ��EF�Գƣ�����APD��ֱ�������Σ���BF�ij�Ϊ_____��
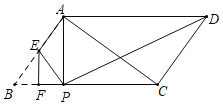
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��3��30�գ��Ĵ�ʡ��ɽ��ľ���ؾ��ڷ���ɭ�ֻ��֣�30�����ҵ��˻�Ӣ�����������˸е�ʹ�ģ�Ҳ�ٴθ����ǵķ���ȫ��ʶ���쾯�ӣ�Ϊ�˼�ǿѧ���ķ���ȫ��ʶ��ijУ������һ�Ρ�����ȫ֪ʶ������������100�֣���������г�ȡ�˲���ѧ���ijɼ����������������������²�������ͳ��ͼ����
��� | �ɼ�x/�� | ����ֵ |
A | 50��x��60 | 55 |
B | 60��x��70 | 65 |
C | 70��x��80 | 75 |
D | 80��x��90 | 85 |
E | 90��x��100 | 95 |
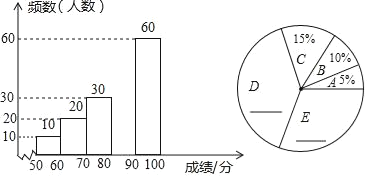
�����ͼ���ṩ����Ϣ��������и��⣺
��1����ȫƵ���ֲ�ֱ��ͼ������ͳ��ͼ��
��2��������80��x��90��Ӧ���ε�Բ�ĽǵĶ������� ���㣬����ȡ��ѧ�������ɼ�����λ�������� �������ڣ�
��3������ÿ�������ֵ�����������˵������ƽ��������������ÿλѧ���ľ����ɼ���������Ƹ�У����ѧ����ƽ���ɼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ������һ���Ͷ�����ij��ѧ��֯�˼ס������������Ͷ�С��������x��������y���������л�·����������·����ɨ���������ݴ�ɨ�����Ľ�����ѧУ��ʱ������������������Ӽ����50��ȥ����������������Ϊ����������2��������������m��ȥ���������������Ϊ����������3����
(1)���x��m֮��ĺ�������ʽ��
(2)�ʣ���mΪ��ֵʱ���������������������Ƕ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
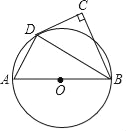
����Ŀ����ͼ��ABΪ��O��ֱ������C�ڡ�O�⣬��ABC��ƽ�������O���ڵ�D����C=90�㣮
��1��CD���O��������λ�ù�ϵ����˵�����ɣ�
��2������CDB=60�㣬AB=6����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
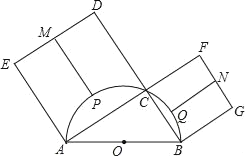
����Ŀ����ͼ��C����ABΪֱ���İ�ԲO��һ�㣬����AC��BC���ֱ���AC��BCΪ��������������ACDE��BCFG��DE��FG, ![]() ���е�ֱ���M��N��P��Q����MP+NQ��14��AC+BC��20����AB�ij��ǣ�������
���е�ֱ���M��N��P��Q����MP+NQ��14��AC+BC��20����AB�ij��ǣ�������
A. 9![]() B.
B. ![]() C. 13D. 16
C. 13D. 16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��x�ύ�ڵ㣨-1��0������������Ϊ��1��m������y�ύ���ڣ�0��3������0��4��֮���������˵㣩���������н��ۣ���3a+b��0����-![]() ��a��-1���۹���x�ķ���ax2+bx+c=m-2����������ȵ�ʵ������������M��-1.5��y1����N��2.5��y2���Ǻ���ͼ���ϵ����㣬��y1=y2��������ȷ���۵ĸ���Ϊ��������
��a��-1���۹���x�ķ���ax2+bx+c=m-2����������ȵ�ʵ������������M��-1.5��y1����N��2.5��y2���Ǻ���ͼ���ϵ����㣬��y1=y2��������ȷ���۵ĸ���Ϊ��������

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
��ͼ1������OAB����OCD�У�OA=OB��OC=OD����AOB=��COD=40��������AC��BD���ڵ�M����գ�
��![]() ��ֵΪ�� ����
��ֵΪ�� ����
�ڡ�AMB�Ķ���Ϊ�� ����
��2�����̽��
��ͼ2������OAB����OCD�У���AOB=��COD=90�㣬��OAB=��OCD=30��������AC��BD���ӳ����ڵ�M�����ж�![]() ��ֵ����AMB�Ķ�������˵�����ɣ�
��ֵ����AMB�Ķ�������˵�����ɣ�
��3����չ����
�ڣ�2���������£�����OCD�Ƶ�O��ƽ������ת��AC��BD����ֱ�߽��ڵ�M����OD=1��OB=![]() ����ֱ��д������C���M�غ�ʱAC�ij���
����ֱ��д������C���M�غ�ʱAC�ij���

���𰸡���1����1����40�㣻��2��![]() ��90�㣻��3��AC�ij�Ϊ3
��90�㣻��3��AC�ij�Ϊ3![]() ��2
��2![]() ��
��
��������
��1����֤����COA�ա�DOB��SAS������AC=BD����ֵΪ1��
���ɡ�COA�ա�DOB���á�CAO=��DBO�����������ε��ڽǺͶ����ã���AMB=180��-����DBO+��OAB+��ABD��=180��-140��=40�㣻
��2���������ߵı�����Ҽн���ȿɵá�AOC�ס�BOD����![]() ����ȫ�������ε����ʵá�AMB�Ķ�����
����ȫ�������ε����ʵá�AMB�Ķ�����
��3����ȷ��ͼ�Σ�����C���M�غ�ʱ���������������ͼ3��4��ͬ���ɵã���AOC�ס�BOD�����AMB=90�㣬![]() ���ɵ�AC�ij���
���ɵ�AC�ij���
��1�����ⷢ�֣�
����ͼ1��

�ߡ�AOB=��COD=40�㣬
���COA=��DOB��
��OC=OD��OA=OB��
���COA�ա�DOB��SAS����
��AC=BD��
��![]()
�ڡߡ�COA�ա�DOB��
���CAO=��DBO��
�ߡ�AOB=40�㣬
���OAB+��ABO=140�㣬
�ڡ�AMB�У���AMB=180��-����CAO+��OAB+��ABD��=180��-����DBO+��OAB+��ABD��=180��-140��=40�㣬
��2�����̽����
��ͼ2��![]() ����AMB=90�㣬�����ǣ�
����AMB=90�㣬�����ǣ�
Rt��COD�У���DCO=30�㣬��DOC=90�㣬
��![]() ��
��
ͬ���ã�![]() ��
��
��![]() ��
��
�ߡ�AOB=��COD=90�㣬
���AOC=��BOD��
���AOC�ס�BOD��
��![]() ����CAO=��DBO��
����CAO=��DBO��
�ڡ�AMB�У���AMB=180��-����MAB+��ABM��=180��-����OAB+��ABM+��DBO��=90�㣻
��3����չ���죺
�ٵ�C���M�غ�ʱ����ͼ3��
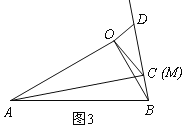
ͬ���ã���AOC�ס�BOD��
���AMB=90�㣬![]() ��
��
��BD=x����AC=![]() x��
x��
Rt��COD�У���OCD=30�㣬OD=1��
��CD=2��BC=x-2��
Rt��AOB�У���OAB=30�㣬OB=![]() ��
��
��AB=2OB=2![]() ��
��
��Rt��AMB�У��ɹ��ɶ����ã�AC2+BC2=AB2��
(![]() x)2+(x2)2��(2
x)2+(x2)2��(2![]() )2��
)2��
x2-x-6=0��
��x-3����x+2��=0��
x1=3��x2=-2��
��AC=3![]() ��
��
�ڵ�C���M�غ�ʱ����ͼ4��
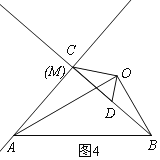
ͬ���ã���AMB=90�㣬![]() ��
��
��BD=x����AC=![]() x��
x��
��Rt��AMB�У��ɹ��ɶ����ã�AC2+BC2=AB2��
(![]() x)2+��x+2��2=(2
x)2+��x+2��2=(2![]() )2.
)2.
x2+x-6=0��
��x+3����x-2��=0��
x1=-3��x2=2��
��AC=2![]() ��.
��.
����������AC�ij�Ϊ3![]() ��2
��2![]() ��
��
�㾦�������������ε��ۺ��⣬��Ҫ������������ȫ�Ⱥ����Ƶ����ʺ��ж������α任���⣬����Ĺؼ����ܵó�����AOC�ס�BOD���������������ε����ʣ���������ȵ�˼�������⣬������һ���ȽϺõ���Ŀ��
�����͡������
��������
25
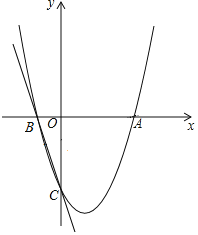
����Ŀ����ͼ����֪������y��ax2+bx��3��a��0��������A��3��0����B����1��0����
��1����������ߵĽ���ʽ��
��2�����Ե�AΪԲ�ĵ�Բ��ֱ��BC�����ڵ�M�����е�M�����ꣻ
��3������Q��x���ϣ���P���������ϣ��Ƿ�����Ե�B��C��Q��PΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com