
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮAOBCЕФЖЅЕуCЕФзјБъЪЧЃЈ6ЃЌ4ЃЉЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЯпЖЮACдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШбиЯпЖЮBOдЫЖЏЃЌЕБQЕНДяOЕуЪБЃЌPЃЌQЭЌЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЪЧtУыЃЈtЃО0ЃЉЃЎ
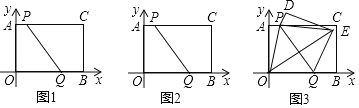
ЃЈ1ЃЉШчЭМ1ЃЌЕБЪБМфtЃНЁЁ УыЪБЃЌЫФБпаЮAPQOЪЧОиаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкPЃЌQдЫЖЏЙ§ГЬжаЃЌЕБPQЃН5ЪБЃЌЪБМфtЕШгкЁЁ УыЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБPЃЌQдЫЖЏЕНЭМжаЮЛжУЪБЃЌНЋОиаЮбиPQелЕўЃЌЕуAЃЌOЕФЖдгІЕуЗжБ№ЪЧDЃЌEЃЌСЌНгOPЃЌOEЃЌДЫЪБЁЯPOEЃН45ЁуЃЌСЌНгPEЃЌЧѓжБЯпOEЕФКЏЪ§БэДяЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉtЃН2ЃЛЃЈ2ЃЉ1Лђ3ЃЛЃЈ3ЃЉyЃН![]() xЃЎ
xЃЎ
ЁОНтЮіЁП
ЯШИљОнЬтвтгУtБэЪОAPЁЂBQЁЂPCЁЂOQЕФГЄЃЎ
ЃЈ1ЃЉгЩЫФБпаЮAPQOЪЧОиаЮПЩЕУAPЃНOQЃЌСаЕУЗНГЬМДПЩЧѓГіtЃЎ
ЃЈ2ЃЉЙ§ЕуPзїxжсЕФДЙЯпPHЃЌЙЙдьжБНЧЁїPQHЃЌЧѓЕУHQЕФжЕЃЎгЩЕуHЁЂQЮЛжУВЛЭЌЗжСНжжЧщПіЬжТлгУtБэЪОHQЃЌМДСаЕУЗНГЬЧѓГіtЃЎИљОнtЕФШЁжЕЗЖЮЇПМТЧtЕФКЯРэадЃЎ
ЃЈ3ЃЉгЩжсЖдГЦаджЪЃЌЖдГЦжсPQДЙжБЦНЗжЖдгІЕуСЌЯпOCЃЌЕУOPЃНPEЃЌQEЃНOQЃЎгЩЁЯPOEЃН45ЁуПЩЕУЁїOPEЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯOPEЃН90ЁуЃЌМДЕуEдкОиаЮAOBCФкВПЃЌЮоаыЗжРрЬжТлЃЎвЊЧѓЕуEзјБъЙЪЙ§ЕуEзїxжсДЙЯпMNЃЌвзжЄЁїMPEЁеЁїAOPЃЌгЩЖдгІБпЯрЕШПЩгУtБэЪОENЃЌQNЃЎдкжБНЧЁїENQжаРћгУЙДЙЩЖЈРэЮЊЕШСПЙиЯЕСаЗНГЬМДЧѓГіtЃЎ
ЁпОиаЮAOBCжаЃЌCЃЈ6ЃЌ4ЃЉ
ЁрOBЃНACЃН6ЃЌBCЃНOAЃН4
вРЬтвтЕУЃКAPЃНtЃЌBQЃН2tЃЈ0ЃМtЁм3ЃЉ
ЁрPCЃНACЉAPЃН6ЉtЃЌOQЃНOBЉBQЃН6Љ2t
ЃЈ1ЃЉЁпЫФБпаЮAPQOЪЧОиаЮ
ЁрAPЃНOQ
ЁрtЃН6Љ2t
НтЕУЃКtЃН2
ЙЪД№АИЮЊЃК2ЃЎ
ЃЈ2ЃЉЙ§ЕуPзїPHЁЭxжсгкЕуH
ЁрЫФБпаЮAPHOЪЧОиаЮ
ЁрPHЃНOAЃН4ЃЌOHЃНAPЃНtЃЌЁЯPHQЃН90Ёу
ЁпPQЃН5
ЁрHQЃН![]()
ЂйШчЭМ1ЃЌШєЕуHдкЕуQзѓВрЃЌдђHQЃНOQЉOHЃН6Љ3t
Ёр6Љ3tЃН3
НтЕУЃКtЃН1
ЂкШчЭМ2ЃЌШєЕуHдкЕуQгвВрЃЌдђHQЃНOHЉOQЃН3tЉ6
Ёр3tЉ6ЃН3
НтЕУЃКtЃН3
ЙЪД№АИЮЊЃК1Лђ3ЃЎ
ЃЈ3ЃЉЙ§ЕуEзїMNЁЭxжсгкЕуNЃЌНЛACгкЕуM
ЁрЫФБпаЮAMNOЪЧОиаЮ
ЁрMNЃНOAЃН4ЃЌONЃНAM
ЁпОиаЮбиPQелЕўЃЌЕуAЃЌOЕФЖдгІЕуЗжБ№ЪЧDЃЌE
ЁрPQДЙжБЦНЗжOE
ЁрEQЃНOQЃН6Љ2tЃЌPOЃНPE
ЁпЁЯPOEЃН45Ёу
ЁрЁЯPEOЃНЁЯPOEЃН45Ёу
ЁрЁЯOPEЃН90ЁуЃЌЕуEдкОиаЮAOBCФкВП
ЁрЁЯAPO+ЁЯMPEЃНЁЯAPO+ЁЯAOPЃН90Ёу
ЁрЁЯMPEЃНЁЯAOP
дкЁїMPEгыЁїAOPжа

ЁрЁїMPEЁеЁїAOPЃЈAASЃЉ
ЁрPMЃНOAЃН4ЃЌMEЃНAPЃНt
ЁрONЃНAMЃНAP+PMЃНt+4ЃЌENЃНMNЉMEЃН4Љt
ЁрQNЃНONЉOQЃНt+4ЉЃЈ6Љ2tЃЉЃН3tЉ2
ЁпдкRtЁїENQжаЃЌEN2+QN2ЃНEQ2
ЁрЃЈ4ЉtЃЉ2+ЃЈ3tЉ2ЃЉ2ЃНЃЈ6Љ2tЃЉ2
НтЕУЃКt1ЃНЉ2ЃЈЩсШЅЃЉЃЌt2ЃН![]()
ЁрAMЃН![]() +4ЃН
+4ЃН![]() ЃЌENЃН4Љ
ЃЌENЃН4Љ![]() ЃН
ЃН![]()
ЁрЕуEзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁржБЯпOEЕФКЏЪ§БэДяЪНЮЊyЃН![]() xЃЎ
xЃЎ





 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊCBЃНCAЃЌЁЯACBЃН90ЁуЃЌЕуDдкБпBCЩЯЃЈгыBЃЌCВЛжиКЯЃЉЃЌЫФБпаЮADEFЮЊе§ЗНаЮЃЌЙ§ЕуFзїFGЁЭCAЃЌНЛCAЕФбгГЄЯпгкЕуGЃЌСЌНгFBЃЌНЛDEгкЕуQЃЌЕУГівдЯТНсТлЃКЂйACЃНFGЃЛЂкSЁїFABЃКSЫФБпаЮCBFGЃН1ЃК2ЃЛЂлЁЯABCЃНЁЯABFЃЛЂмAD2ЃНFQACЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
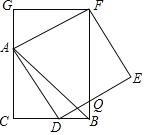
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁАбЇЯАРзЗцЛюЖЏдТЁБжаЃЌФГаЃОХЃЈ2ЃЉАрШЋАрЭЌбЇЖМВЮМгСЫЁАЙуИцЧхГ§ЁЂжњРЯжњВаЁЂЧхРэРЌЛјЁЂвхЮёжВЪїЁБЫФИіжОдИЛюЖЏЃЈУПШЫжЛВЮМгвЛИіЛюЖЏЃЉЃЎЮЊСЫСЫНтЧщПіЃЌаЁУїЪеМЏећРэЯрЙиЕФЪ§ОнКѓЃЌЛцжЦШчЭМЫљЪОЃЌВЛЭъећЕФЭГМЦЭМЃЎЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЧѓИУАрЕФШЫЪ§ЃЛ
ЃЈ2ЃЉЧыАбелЯпЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЧѓЩШаЮЭГМЦЭМжаЃЌЙуИцЧхГ§ВПЗжЖдгІЕФдВаФНЧЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
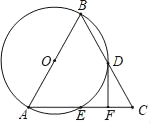
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌвдABЮЊжБОЖЕФЁбOЗжБ№гыBCЃЌACЯрНЛгкЕуDЃЌEЃЌBDЃНCDЃЌЙ§ЕуDзїЁбOЕФЧаЯпНЛБпACгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКDFЁЭACЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌCFЃН1ЃЌЧѓ![]() ЕФГЄЃЈНсЙћБЃСєІаЃЉЃЎ
ЕФГЄЃЈНсЙћБЃСєІаЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
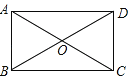
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌОиаЮABCDЃЌABЃН2ЃЌBCЃН4ЃЌЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌЕуPдкЖдНЧЯпBDЩЯЃЌВЂЧвAЃЌOЃЌPзщГЩвдOPЮЊбќЕФЕШбќШ§НЧаЮЃЌФЧУДOPЕФГЄЕШгк___ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪадЄВтФГвћСЯгаЗЂеЙЧАЭОЃЌгУ1600дЊЙКНјвЛХњвћСЯЃЌУцЪаКѓЙћШЛЙЉВЛгІЧѓЃЌгжгУ6000дЊЙКНјетХњвћСЯЃЌЕкЖўХњвћСЯЕФЪ§СПЪЧЕквЛХњЕФ3БЖЃЌЕЋЕЅМлБШЕквЛХњЙѓ2дЊ.
(1)ЕквЛХњвћСЯНјЛѕЕЅМлЖрЩйдЊЃП
(2)ШєЖўДЮЙКНјвћСЯАДЭЌвЛМлИёЯњЪлЃЌСНХњШЋВПЪлЭъКѓЃЌЛёРћВЛЩйгк1200дЊЃЌФЧУДЯњЪлЕЅМлжСЩйЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
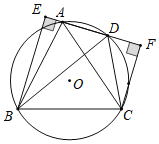
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧе§ЁїABCЕФЭтНгдВЃЌЕуDЮЊдВЩЯвЛЕуЃЌСЌНгADЃЌЗжБ№Й§ЕуBКЭЕуCзїADбгГЄЯпЕФДЙЯпЃЌДЙзуЗжБ№ЮЊЕуEКЭЕуFЃЌСЌНгBDЁЂCDЃЌвбжЊEB=3ЃЌFC=2ЃЌЯждкгаШчЯТ4ИіНсТлЃКЂйЁЯCDF=60ЁуЃЛЂкЁїEDBЁзЁїFDCЃЛЂлBC=![]() ЃЛЂм
ЃЛЂм![]() ЃЌЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉИі
ЃЌЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁЃЉИі
A. 1
B. 2
C. 3
D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩЭжаЛЊЪЋДЪЃЌбАЮФЛЏЛљвђЃЌЦЗЩњЛюжЎУРЁБЃЌФГаЃОйАьСЫЪзНьЁАжаЙњЪЋДЪДѓЛсЁБЃЌШЋаЃЭЌЪБФЌаД50ЪзЙХЪЋДЪЃЌУПе§ШЗФЌаДГівЛЪзЙХЪЋДЪЕУ2ЗжЃЌНсЙћга500УћНјШыОіШќЃЌДгет500УћЕФбЇЩњжаЫцЛњГщШЁ50УћбЇЩњНјааГЩМЈЗжЮіЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃКЃЈзюИпЗж98ЗжЃЉЃК
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 50ЁмxЃМ60 | 6 |
Ек2зщ | 60ЁмxЃМ70 | 8 |
Ек3зщ | 70ЁмxЃМ80 | 14 |
Ек4зщ | 80ЁмxЃМ90 | a |
Ек5зщ | 90ЁмxЃМ100 | 10 |
ЂёЃЎЕк3зщЕФОпЬхЗжЪ§ЮЊЃК70ЃЌ70ЃЌ70ЃЌ72ЃЌ72ЃЌ74ЃЌ74ЃЌ74ЃЌ76ЃЌ76ЃЌ78ЃЌ78ЃЌ78ЃЌ78
Ђђ.50ШЫЕУЗжЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчБэЃК
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | |
ЕУЗжЃЈЗжЃЉ | m | n |
ЧыНсКЯЭМБэЪ§ОнаХЯЂЭъГЩЯТСаИїЬтЃК
ЃЈ1ЃЉЬюПеaЃНЁЁ ЁЁЃЌmЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєВтЪдГЩМЈВЛЕЭгк80ЗжЮЊгХауЃЌЙРМЦНјШыОіШќЕФБОДЮВтЪдЮЊЕФгХауЕФбЇЩњгаЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХаТФмдДЦћГЕЕФЗЂеЙЃЌФГЙЋНЛЙЋЫОНЋгУаТФмдДЙЋНЛГЕЬдЬФГвЛЬѕЯпТЗЩЯЁАУАКкбЬЁБНЯбЯжиЕФШМгЭЙЋНЛГЕЃЌМЦЛЎЙКТђAаЭКЭBаЭаТФмдДЙЋНЛГЕЙВ10СОЃЌШєЙКТђAаЭЙЋНЛГЕ1СОЃЌBаЭЙЋНЛГЕ2СОЃЌЙВаш300ЭђдЊЃЛШєЙКТђAаЭЙЋНЛГЕ2СОЃЌBаЭЙЋНЛГЕ1СОЃЌЙВаш270ЭђдЊЃЌ
(1)ЧѓЙКТђAаЭКЭBаЭЙЋНЛГЕУПСОИїашЖрЩйЭђдЊЃП
(2)дЄМЦдкИУЬѕЯпТЗЩЯAаЭКЭBаЭЙЋНЛГЕУПСОФъОљдиПЭСПЗжБ№ЮЊ80ЭђШЫДЮКЭ100ЭђШЫДЮЃЎШєИУЙЋЫОЙКТђAаЭКЭBаЭЙЋНЛГЕЕФзмЗбгУВЛГЌЙ§1000ЭђдЊЃЌЧвШЗБЃет10СОЙЋНЛГЕдкИУЯпТЗЕФФъОљдиПЭСПзмКЭВЛЩйгк900ЭђШЫДЮЃЌдђИУЙЋЫОгаФФМИжжЙКГЕЗНАИЃПФФжжЙКГЕЗНАИзмЗбгУзюЩйЃПзюЩйзмЗбгУЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com