
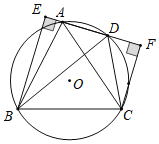
【题目】如图,⊙O是正△ABC的外接圆,点D为圆上一点,连接AD,分别过点B和点C作AD延长线的垂线,垂足分别为点E和点F,连接BD、CD,已知EB=3,FC=2,现在有如下4个结论:①∠CDF=60°;②△EDB∽△FDC;③BC=![]() ;④
;④![]() ,其中正确的结论有( )个
,其中正确的结论有( )个
A. 1
B. 2
C. 3
D. 4
【答案】B
【解析】
根据等边三角形的性质,相似三角形的判定和性质,解直角三角形等知识一一判断即可.
解:∵△ABC是等边三角形
∴∠ABC=∠ACB=∠BAC=60°,
∵A、B、C、D四点共圆,
∴∠CDF=∠ABC=60°,故①正确.
∵∠BDE=∠ACB=60°,
∴∠BDE=∠CDF=60°,
∵BE⊥AD,CF⊥AD,
∴∠E=∠F=90°,
∴△EDB∽△FDC,故②正确.
∵BE=![]() DE=3,CF=
DE=3,CF=![]() DF=2,
DF=2,
∴DE=![]() ,DF=
,DF=![]() ,
,
∴EF=DE+DF=![]() . 过点C作CG⊥BE于点G.
. 过点C作CG⊥BE于点G.
∴四边形EGCF是矩形,
∴EG=FC=2,CG=EF=![]() ,
,
∴BG=BE-EG=1.
在Rt△BGC中,由勾股定理可得:BC=![]() ,故③错误.
,故③错误.
在Rt△AEB中,由勾股定理可得:AE=![]() ,
,
∴AD=DE-AE=![]() ,
,
∴AD:DE=2:3.
∴S△ADB=![]() S△EDB,故④错误.
S△EDB,故④错误.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
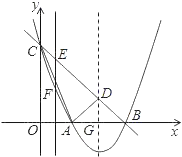
【题目】如图,顶点坐标为(2,﹣1)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的表达式;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
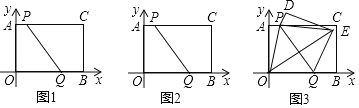
【题目】已知:如图,在平面直角坐标系中,矩形AOBC的顶点C的坐标是(6,4),动点P从点A出发,以每秒1个单位的速度沿线段AC运动,同时动点Q从点B出发,以每秒2个单位的速度沿线段BO运动,当Q到达O点时,P,Q同时停止运动,运动时间是t秒(t>0).
(1)如图1,当时间t= 秒时,四边形APQO是矩形;
(2)如图2,在P,Q运动过程中,当PQ=5时,时间t等于 秒;
(3)如图3,当P,Q运动到图中位置时,将矩形沿PQ折叠,点A,O的对应点分别是D,E,连接OP,OE,此时∠POE=45°,连接PE,求直线OE的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
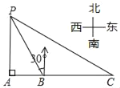
【题目】如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
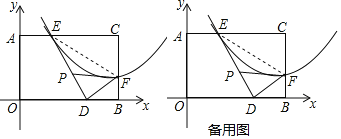
【题目】如图,在平面直角坐标系中,抛物线与矩形AOBC的边AC、BC分别交于点E,F,E(3,4),且F(8,![]() )为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
)为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
(1)求该抛物线的解析式;
(2)点P为线段ED上一动点,连接PF,当PF平分∠EFD时,求PD的长度;
(3)四边形AODE以1个单位/秒的速度沿着x轴向右运动,当点E与点C重合时停止运动,设运动时间为t秒,运动后的四边形A′O′D′E′与△DEF重合部分的面积为S,请直接写出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+ax+nb=0(1≤n≤3,n为整数),其中a是从2、4、6三个数中任取的一个数,b是从1、3、5三个数中任取的一个数,定义“方程有实数根”为事件An(n=1,2,3),当An的概率最小时,n的所有可能值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com