
【题目】赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,全校同时默写50首古诗词,每正确默写出一首古诗词得2分,结果有500名进入决赛,从这500名的学生中随机抽取50名学生进行成绩分析,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:(最高分98分):
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
Ⅰ.第3组的具体分数为:70,70,70,72,72,74,74,74,76,76,78,78,78,78
Ⅱ.50人得分平均数、中位数、众数如表:
平均数 | 中位数 | 众数 | |
得分(分) | m | n |
请结合图表数据信息完成下列各题:
(1)填空a= ,m= ;
(2)将频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,估计进入决赛的本次测试为的优秀的学生有多少?

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
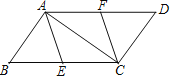
【题目】已知点E、F分别是ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,求AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
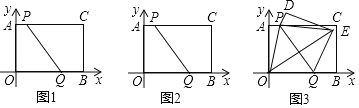
【题目】已知:如图,在平面直角坐标系中,矩形AOBC的顶点C的坐标是(6,4),动点P从点A出发,以每秒1个单位的速度沿线段AC运动,同时动点Q从点B出发,以每秒2个单位的速度沿线段BO运动,当Q到达O点时,P,Q同时停止运动,运动时间是t秒(t>0).
(1)如图1,当时间t= 秒时,四边形APQO是矩形;
(2)如图2,在P,Q运动过程中,当PQ=5时,时间t等于 秒;
(3)如图3,当P,Q运动到图中位置时,将矩形沿PQ折叠,点A,O的对应点分别是D,E,连接OP,OE,此时∠POE=45°,连接PE,求直线OE的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
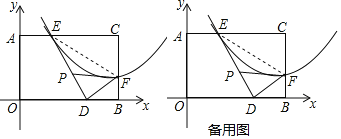
【题目】如图,在平面直角坐标系中,抛物线与矩形AOBC的边AC、BC分别交于点E,F,E(3,4),且F(8,![]() )为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
)为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
(1)求该抛物线的解析式;
(2)点P为线段ED上一动点,连接PF,当PF平分∠EFD时,求PD的长度;
(3)四边形AODE以1个单位/秒的速度沿着x轴向右运动,当点E与点C重合时停止运动,设运动时间为t秒,运动后的四边形A′O′D′E′与△DEF重合部分的面积为S,请直接写出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点O在△ABC的BC边上,⊙O经过点A、C,且与BC相交于点 D.点E是下半圆弧的中点,连接AE交BC于点F,已知AB=BF.
(1)求证:AB是⊙O的切线;
(2)若OC=3,OF=1,求cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
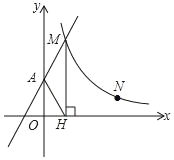
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求H点的坐标及k的值;
(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是一个地球仪及它的平面图,在平面图中,点A、B分别为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所夹的角度约为67°,半径OC所在的直线与放置它的平面垂直,垂足为点E,DE=15cm,AD=14cm.

(1)求半径OA的长(结果精确到0.1cm,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
(2)求扇形BOC的面积(π取3.14,结果精确到1cm)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com