
【题目】 如图,点O在△ABC的BC边上,⊙O经过点A、C,且与BC相交于点 D.点E是下半圆弧的中点,连接AE交BC于点F,已知AB=BF.
(1)求证:AB是⊙O的切线;
(2)若OC=3,OF=1,求cosB的值.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据垂径定理求出∠EOF=90°,根据等腰三角形性质求出∠BAF=∠BFA,∠E=∠OAE,求出∠OAE+∠BAF=90°,根据切线的判定得出即可;
(2)设AB=x,则BF=x,OB=x+1,根据勾股定理求出AB的长,解直角三角形求出即可.
(1)证明:连接OA、OE,
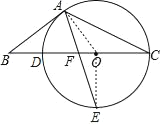
∵点E是下半圆弧的中点,OE过O,
∴OE⊥DC,
∴∠FOE=90°,
∴∠E+∠OFE=90°,
∵OA=OE,AB=BF,
∴∠BAF=∠BFA,∠E=∠OAE,
∵∠AFB=∠OFE,
∴∠OAE+∠BAF=90°,
即OA⊥AB,
∵OA为半径,
∴AB是⊙O的切线;
(2)解:设AB=x,则BF=x,OB=x+1,
∵OA=OC=3,
由勾股定理得:OB2=AB2+OA2,
∴(1+x)2=32+x2,
解得:x=4,
∴cosB=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10cm,cosB=![]() 点M、N分别是边BC和AC上的两个动点,点M以2cm/s的速度沿C→B方向运动,同时点N以1cm/s的速度沿A→C方向运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t,四边形ABMN的面积为S,则下列能大致反映S与t函数关系的图象是( )
点M、N分别是边BC和AC上的两个动点,点M以2cm/s的速度沿C→B方向运动,同时点N以1cm/s的速度沿A→C方向运动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t,四边形ABMN的面积为S,则下列能大致反映S与t函数关系的图象是( )
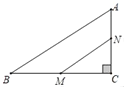
A.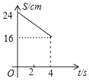 B.
B.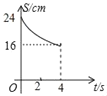 C.
C.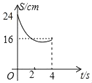 D.
D.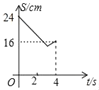
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,全校同时默写50首古诗词,每正确默写出一首古诗词得2分,结果有500名进入决赛,从这500名的学生中随机抽取50名学生进行成绩分析,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:(最高分98分):
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
Ⅰ.第3组的具体分数为:70,70,70,72,72,74,74,74,76,76,78,78,78,78
Ⅱ.50人得分平均数、中位数、众数如表:
平均数 | 中位数 | 众数 | |
得分(分) | m | n |
请结合图表数据信息完成下列各题:
(1)填空a= ,m= ;
(2)将频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,估计进入决赛的本次测试为的优秀的学生有多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC>BC,分别以AB,BC,CA为一边向△ABC外作正方形ABDE、BCMN,CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3.
(1)猜想S1、S2、S3的大小关系.
(2)请对(1)的猜想,任选一个关系进行证明;
(3)若将图1中的Rt△ABC改为图2中的任意△ABC,若SABC=5,求出S1+S2+S3的值;
(4)若将图2中的任意△ABC改为任意凸四边形ABCD,若S△AEG+S△CNK+S△IBH+S△DFM=α,则四边形ABCD的面积为 (直接用含α的代数式表示结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,以二次函数y=ax2+bx+c的二次项系数a的2倍为一次项系数,一次项系数b为常数项构造的一次函数y=2ax+b叫做二次函数y=ax2+bx+c的“子函数”,反过来,二次函数y=ax2+bx+c叫做一次函数y=2ax+b的“母函数”.
(1)若一次函数y=2x-4是二次函数y=ax2+bx+c的“子函数”,且二次函数经过点(3,0),求此二次函数的解析式及顶点坐标.
(2)若“子函数”y=x-6的“母函数”的最小值为1,求“母函数”的函数表达式.
(3)已知二次函数y=-x2-4x+8的“子函数”图象直线l与x轴、y轴交于C、D两点,动点P为二次函数y=-x2-4x+8对称轴右侧上的动点,求△PCD的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com