
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC>BC,分别以AB,BC,CA为一边向△ABC外作正方形ABDE、BCMN,CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3.
(1)猜想S1、S2、S3的大小关系.
(2)请对(1)的猜想,任选一个关系进行证明;
(3)若将图1中的Rt△ABC改为图2中的任意△ABC,若SABC=5,求出S1+S2+S3的值;
(4)若将图2中的任意△ABC改为任意凸四边形ABCD,若S△AEG+S△CNK+S△IBH+S△DFM=α,则四边形ABCD的面积为 (直接用含α的代数式表示结果)

【答案】(1)S1=S2=S3(2)见解析(3)15(4)![]() a
a
【解析】
(1)猜想三个三角形面积相等;
(2)证明三个三角形都与△ABC面积相等.观察图形,要证明面积相等,图中正方形提供了一组相等的边作为底,只要证明高相等即可;
(3)证明思路同(2),S1、S2、S3面积都等于△ABC问题可求;
(4)作四边形ABCD对角线,可以以利用(3)中结论,△AEG、△CNK、△IBH、△DFM的面积可以分别于四边形ABCD被对角线分割所得的三角形对应相等,则问题可证.
(1)猜想:S1=S2=S3
(2)如图1,延长FA,过点E作EH⊥FA于H,
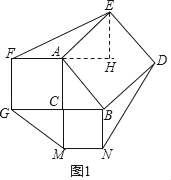
由已知:∠BAE=∠CAH=90°,
∴∠CAB=∠HAE.
∵∠ACB=∠AHE=90°,AE=AB,
∴△HAE≌△CAB,
∴EH=BC,
∴S△AEF=![]() =
=![]() =S△ABC,
=S△ABC,
∴S1=S△ABC,
同理:S2=S△ABC,S3=S△ABC,
∴S1=S2=S3
(3)如图2
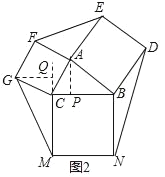
分别过点G和A作GQ⊥MC于Q,AP⊥BC于P,
由已知:∠GCA=∠QCB=90°,
∴∠GCQ=∠ACP.
又∵∠GQC=∠APC=90°,
GC=AC,
∴△GCQ≌△ACP,
∴GQ=AP,
∵S△GCM=![]() ,
,
S△ABC=![]() ,
,
MC=BC,
∴S△GCM=S△ABC,
∴S3=S△ABC,
同理:S1=S△ABC,
S2=S△ABC,
∴S1=S2=S3=S△ABC,
∵SABC=5,
∴S1+S2+S3=15;
(4)如图3,连AC,
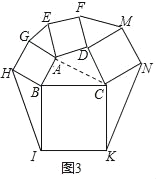
由(3)可知,S△DFM=S△ADC,
S△IBH=S△ABC,
∴S△DFM+S△IBH=S△ADC+S△ABC=S四边形ABCD,
同理:S△AEG+S△CNK=S四边形ABCD,
∴S△AEG+S△CNK+S△IBH+S△DFM=2S四边形ABCD,
∵S△AEG+S△CNK+S△IBH+S△DFM=α,
∴2S四边形ABCD=α,
∴四边形ABCD的面积为![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点O在△ABC的BC边上,⊙O经过点A、C,且与BC相交于点 D.点E是下半圆弧的中点,连接AE交BC于点F,已知AB=BF.
(1)求证:AB是⊙O的切线;
(2)若OC=3,OF=1,求cosB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
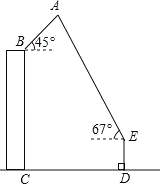
查看答案和解析>>
科目:初中数学 来源: 题型:
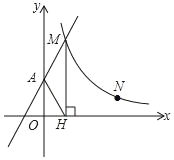
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求H点的坐标及k的值;
(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;
(3)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师为了了解班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查.他将调查结果分为四类:A:很好;B:较好;C:一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
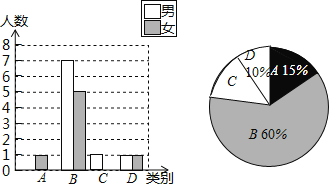
(1)请计算出A类男生和C类女生的人数,并将条形统计图补充完整.
(2)为了共同进步,张老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是⊙O直径,在
是⊙O直径,在![]() 的异侧分别有定点
的异侧分别有定点![]() 和动点
和动点![]() ,如图所示,点
,如图所示,点![]() 在半圆弧
在半圆弧![]() 上运动(不与
上运动(不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 的垂线
的垂线![]() ,交
,交![]() 的延长线于
的延长线于![]() ,已知
,已知![]() ,
,![]() ∶
∶![]() =
=![]() ∶
∶![]() .
.
(1)求证:![]() ·
·![]() =
=![]() ·
·![]() ;
;
(2)当点![]() 运动到
运动到![]() 弧的中点时,求
弧的中点时,求![]() 的长;
的长;
(3)当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?请直接写出这个最大面积.
的面积最大?请直接写出这个最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
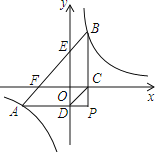
【题目】如图,![]() 的直角顶点P在第四象限,顶点A、B分别落在反比例函数
的直角顶点P在第四象限,顶点A、B分别落在反比例函数![]() 图象的两支上,且
图象的两支上,且![]() 轴于点C,
轴于点C,![]() 轴于点D,AB分别与x轴,y轴相交于点F和
轴于点D,AB分别与x轴,y轴相交于点F和![]() 已知点B的坐标为
已知点B的坐标为![]() .
.
![]() 填空:
填空:![]() ______;
______;
![]() 证明:
证明:![]() ;
;
![]() 当四边形ABCD的面积和
当四边形ABCD的面积和![]() 的面积相等时,求点P的坐标.
的面积相等时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com