
【题目】等腰直角△ABC中,AB=AC,∠BAC=90°,过点B,点C分别作经过点A的直线l的垂线,垂足分别为M、N.
(1)请找到一对全等三角形,并说明理由;
(2)BM,CN,MN之间有何数量关系?并说明理由;
(3)若BM=3,CN=5,求四边形MNCB的面积.

【答案】(1)△ABM≌△CAN,证明见解析;(2)BM+CN=MN,理由见解析;(3)32.
【解析】
(1)根据∠BAC=90°BM⊥MN,得出BM⊥MN,即可证明全等
(2)根据题(1)△ABM≌△CAN,可知CN=AM,BM=AN,即可解答
(3)根据题(2)MN=BM+CN=8,即可解答
(1)△ABM≌△CAN,
理由如下:∵∠BAC=90°,
∴∠MAB+∠NAC=90°,
∵BM⊥MN,
∴∠MAB+∠MBA=90°,
∴∠MBA=∠NAC,
在△ABM和△CAN中,
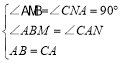 ,
,
∴△ABM≌△CAN;
(2)BM+CN=MN,
理由如下:∵△ABM≌△CAN,
∴CN=AM,BM=AN,
∴MN=AM+AN=BM+CN;
(3)∵BM=3,CN=5,
∴MN=BM+CN=8,
∴四边形MNCB的面积=![]() ×(BM+CN)×MN=
×(BM+CN)×MN=![]() ×(3+5)×8=32.
×(3+5)×8=32.


科目:初中数学 来源: 题型:
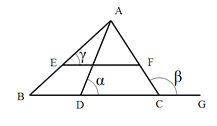
【题目】如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC=3∠BAD,记∠ADC=![]() ,∠ACG=
,∠ACG=![]() ,∠AEF=
,∠AEF=![]() ,则:(1)
,则:(1)![]() __
__![]() (填“>”、“=”或“<”号);
(填“>”、“=”或“<”号);
(2)![]() 、
、![]() 、
、![]() 三者间的数量关系式是_______________.
三者间的数量关系式是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.
与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.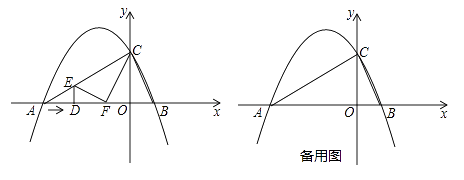
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥EF,∠C=90°,∠B,∠D,∠E三个角的大小分别是x,y,z则x,y,z之间满足的关系式是( )
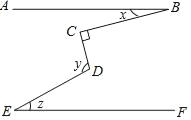
A. x+z=yB. x+y+═180°C. x+y﹣z=90°D. y+z﹣x=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
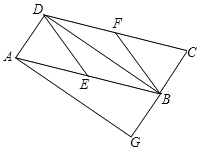
(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,
(1)如图1,若AB∥ON,则
①∠ABO的度数是______;
②当∠BAD=∠ABD时,x=______;
当∠BAD=∠BDA时,x=______;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
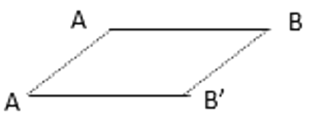
【题目】如图所示,一条线段AB平移一段距离后得到线段A’B’,连接AA’,BB’可以得到一个平行四边形ABB’A’请据此回答下面问题:
在平面直角坐标系中有A点(1,0),B点(-2,1),C点(-1,-3),若坐标平面内存在点D,使得A,B,C,D四点恰好能构成一个平行四边形,求D点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com