
【题目】如图,已知AB∥EF,∠C=90°,∠B,∠D,∠E三个角的大小分别是x,y,z则x,y,z之间满足的关系式是( )
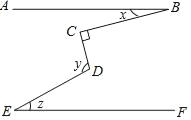
A. x+z=yB. x+y+═180°C. x+y﹣z=90°D. y+z﹣x=180°
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有大小两种货车,已知1辆大货车与3辆小货车一次可以运货14吨,2辆大货车与5辆小货车一次可以运货25吨.
(1)1辆大货车与1辆小货车一次可以运货各多少吨?
(2)1辆大货车一次费用为300元,1辆小货车一次费用为200元,要求两种货车共用10辆,两次完成80吨的运货任务,且总费用不超过5400元,有哪几种用车方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.
例如:2635,x=2+6,y=3+5,因为x=y,所以2635是“和平数”.
(1)请判断:3562 (填“是”或“不是”)“和平数”.
(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题,原命题和它的逆命题都是真命题的是( )
A.若![]() ,则
,则![]()
B.若三角形的三条边分别为![]() ,则这个三角形是直角三角形
,则这个三角形是直角三角形
C.正方形的四条边都相等
D.对角线互相垂直平分的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角△ABC中,AB=AC,∠BAC=90°,过点B,点C分别作经过点A的直线l的垂线,垂足分别为M、N.
(1)请找到一对全等三角形,并说明理由;
(2)BM,CN,MN之间有何数量关系?并说明理由;
(3)若BM=3,CN=5,求四边形MNCB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )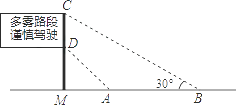
A.4 ![]() 米
米
B.(2 ![]() +2)米
+2)米
C.(4 ![]() ﹣4)米
﹣4)米
D.(4 ![]() ﹣4)米
﹣4)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com