
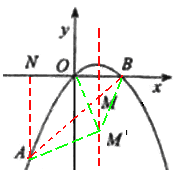
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.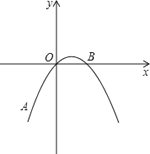
【答案】解:(1)把A(﹣2,﹣4),O(0,0),B(2,0)三点的坐标代入y=ax2+bx+c中,得
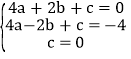 ,解这个方程组,得
,解这个方程组,得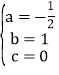 。
。
∴抛物线的解析式为y=﹣![]() x2+x。
x2+x。
(2)由y=﹣![]() x2+x=﹣
x2+x=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,可得
,可得
抛物线的对称轴为x=1,并且对称轴垂直平分线段OB。
∴OM=BM。∴OM+AM=BM+AM。
连接AB交直线x=1于M点,则此时OM+AM最小。
过点A作AN⊥x轴于点N,
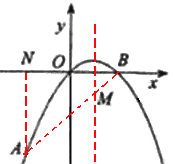
在Rt△ABN中,![]() ,
,
因此OM+AM最小值为![]() 。
。
【解析】
二次函数综合题,曲线上点的坐标与方程的关系,解方程组,二次函数的性质,线段中垂线的性质,三角形三边关系,勾股定理。
(2)根据O、B点的坐标发现:抛物线上,O、B两点正好关于抛物线的对称轴对称,那么只需连接A、B,直线AB和抛物线对称轴的交点即为符合要求的M点,而AM+OM的最小值正好是AB的长。
对x=1上其它任一点M′,根据三角形两边之和大于第三边的性质,总有:
O M′+A M′=" B" M′+A M′>AB=OM+AM,
即OM+AM为最小值。


科目:初中数学 来源: 题型:
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
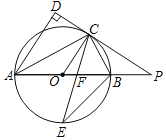
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凤城商场经销一种高档水果,售价为每千克50元
(1)连续两次降价后售价为每千克32元,若每次下降的百分率相同.求平均下降的百分率;
(2)已知这种水果的进价为每千克40元,每天可售出500千克,经市场调查发现,若每千克涨价1元,日销售量将减少20千克,每千克应涨价多少元才能使每天获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
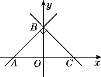
【题目】如图,直线y=x+2与x轴交于点A,与y轴交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax2+bx+c以C为顶点,且经过点B,求这条抛物线对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地开展选修课,戏剧社的张老师统计了近五年该社团学生参加市级比赛的获奖情况,并绘制成如下两幅不完整的统计图,请根据图中的信息,完成下列问题:

![]() 该社团2017年获奖学生人数占近五年获奖总人数的百分比为_____,补全折线统计图;
该社团2017年获奖学生人数占近五年获奖总人数的百分比为_____,补全折线统计图;
![]() 该社团2017年获奖学生中,初一、初二年级各有一名学生,其余全是初三年级学生,张老师打算从2017年获奖学生中随机抽取两名学生参加学校的艺术节表演,请你用列表法或画树状图的方法,求出所抽取两名学生恰好都来自初三年级的概率.
该社团2017年获奖学生中,初一、初二年级各有一名学生,其余全是初三年级学生,张老师打算从2017年获奖学生中随机抽取两名学生参加学校的艺术节表演,请你用列表法或画树状图的方法,求出所抽取两名学生恰好都来自初三年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com