
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t(s).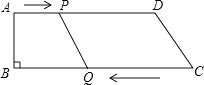
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
【答案】
(1)解:根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t.
∵AD∥BC,
即PD∥CQ,
∴当PD=CQ时,四边形PQCD为平行四边形,
即24﹣t=3t,
解得:t=6,
即当t=6时,PQ∥CD;
(2)解:若PQ=DC,分两种情况:
①PD=QC,由(1)可知,t=6,
②PD≠CQ,则四边形PDCQ是等腰梯形,则有QC=PD+2(BC﹣AD),
可得方程:3t=24﹣t+4,
解得:t=7.
【解析】(1)根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t.根据一组对边平行且相等得四边形是平行四边形得出方程,求解得出t的值,然后根据平行四边形的性质定理得出结论;
(2)若PQ=DC,分两种情况:①PQ=DC,由(1)可知,t=6,②PD≠CQ,则四边形PDCQ是等腰梯形,则有QC=PD+2(BC﹣AD),得出方程求解即可。
【考点精析】关于本题考查的平行四边形的判定与性质和直角梯形,需要了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;一腰垂直于底的梯形是直角梯形才能得出正确答案.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 任意抛掷一个啤酒瓶盖,落地后印有商标一面向上的可能性大小是![]()
B. 一个转盘被分成8块全等的扇形区域,其中2块是红色,6块是蓝色. 用力转动转盘,当转盘停止后,指针对准红色区域的可能性大小是![]()
C. 一个不透明的盒子中装有2个白球,3个红球,这些球除颜色外都相同. 从这个盒子中随意摸出一个球,摸到白球的可能性大小是![]()
D. 100件同种产品中,有3件次品. 质检员从中随机取出一件进行检测,他取出次品的可能性大小是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为 cm.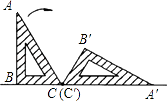
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校植物园沿路护栏的纹饰部分准备设计成若干个形状、大小完全相同的四边形图案,每平移一个图案,纹饰长度就增加![]() cm(如图)所示,已知每个四边形图案的水平方向的对角线长30cm.
cm(如图)所示,已知每个四边形图案的水平方向的对角线长30cm.
(1)若![]() =26cm,且该纹饰要用231个四边形图案,求纹饰的长度
=26cm,且该纹饰要用231个四边形图案,求纹饰的长度![]() ;
;
(2)当![]() =20cm时,若保持(1)中纹饰长度不变,则需要多少个这样的四边形图案?
=20cm时,若保持(1)中纹饰长度不变,则需要多少个这样的四边形图案?
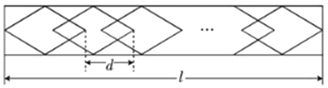
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;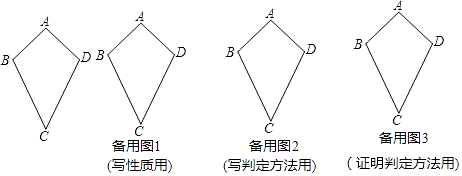
我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
(1)写出筝形的两个性质(定义除外);
(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由:
∵BD平分∠ABC(已知)
∴__________=__________(__________)
又∠1=∠D(已知)
∴__________=__________(__________)
∴__________∥__________(__________)
∴∠ABC+__________=180°(__________)
又∠ABC=55°(已知)
∴∠BCD=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )

A.①②③ B.①③④ C.①②④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com