
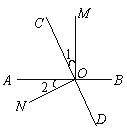
【题目】如图,直线AB,CD相交于O点,OM⊥AB.
(1)若∠1=∠2,求∠NOD;
(2)若∠1=![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
【答案】(1)90°;(2)∠AOC=60°,∠MOD=150°.
【解析】(1)根据垂直的定义,可得∠AOC+∠1=90°由此易推出∠CON=90°,进而结合平角的定义即可解答本题;
(2)根据垂直可知∠AOM=∠BOM=90°,结合∠1=![]() ∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
∠BOC,可得∠1=30°,由此可以得到∠AOC与MOD的度数.
解:(1)∵OM⊥AB,
∴∠AOM=90°,即∠AOC+∠1=90°.
∵∠1=∠2,∠AOC+∠1=90°,
∴∠AOC+∠2=90°,
即∠CON=90°,
∵∠CON+∠NOD=180°,
∴∠NOD=90°.
(2)∵OM⊥AB,
∴∠AOM=∠BOM=90°.
∵∠BOC=∠BOM+∠1,∠BOM=90°,∠1=![]() ∠BOC,
∠BOC,
∴∠1=30°.
∵∠AOC+∠1=∠AOM=90°,∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠MOD=∠MOB+∠AOC=150°.


科目:初中数学 来源: 题型:
【题目】如图已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由(根据解题的要求,在横线处或括号内填写适当的内容或理由).
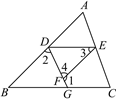
解:∠AED=∠C.
理由如下:
∵∠1+∠4=180°,∠1+∠2=180°,
∴∠2=∠4,∴AB∥EF,
∴________________(两直线平行,内错角相等).
又∵∠3=∠B,∴∠B=∠ADE,
∴DE∥BC(____________________________),
∴∠AED=∠C(__________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点D,DE垂直平分AB,垂足为E,若BC=3,则AD的长为( )
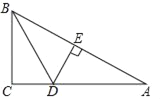
A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com