
【题目】彩虹服装店用![]() 元购进
元购进![]() 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件![]() 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元).他卖完这
(单位:元).他卖完这![]() 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,某校为了营造读书好、好读书、读好书的书香校园,决定采购《简·爱》、《小词大雅》两种图书供学生阅读,通过了解,购买2本《简·爱》和3本《小词大雅》共需168元,购买3本《简·爱》和2本《小词大雅》共需172元.
(1)求一本《简·爱》和《小词大雅》的价格分别是多少元;
(2)若该校计划购买两种图书共300本,其中《简·爱》的数量不多于《小词大雅》数量,且不少于100件.购买《简·爱》m本,求总费用W元与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,学校在团购书籍时,商家店铺中《简·爱》正进行书籍促销活动,每本书箱降价a元(0< a <8),求学校购书的的最低总费用W1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

【答案】(1)b=﹣2a,顶点D的坐标为(﹣![]() ,﹣
,﹣![]() );(2)
);(2)![]() ;(3) 2≤t<
;(3) 2≤t<![]() .
.
【解析】试题分析:(1)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点D的坐标;
(2)把点![]() 代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得
代入直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,可求得另一交点N的坐标,根据a<b,判断a<0,确定D、M、N的位置,画图1,根据面积和可得![]() 的面积即可;
的面积即可;
(3)先根据a的值确定抛物线的解析式,画出图2,先联立方程组可求得当GH与抛物线只有一个公共点时,t的值,再确定当线段一个端点在抛物线上时,t的值,可得:线段GH与抛物线有两个不同的公共点时t的取值范围.
试题解析:(1)∵抛物线![]() 有一个公共点M(1,0),
有一个公共点M(1,0),
∴a+a+b=0,即b=2a,
![]()
∴抛物线顶点D的坐标为![]()
(2)∵直线y=2x+m经过点M(1,0),
∴0=2×1+m,解得m=2,
∴y=2x2,
则![]()
得![]()
∴(x1)(ax+2a2)=0,
解得x=1或![]()
∴N点坐标为![]()
∵a<b,即a<2a,
∴a<0,
如图1,设抛物线对称轴交直线于点E,

∵抛物线对称轴为![]()

![]()
设△DMN的面积为S,
![]()
(3)当a=1时,
抛物线的解析式为:![]()
有![]()
![]()
解得:![]()
∴G(1,2),
∵点G、H关于原点对称,
∴H(1,2),
设直线GH平移后的解析式为:y=2x+t,
x2x+2=2x+t,
x2x2+t=0,
△=14(t2)=0,
![]() 当点H平移后落在抛物线上时,坐标为(1,0),
当点H平移后落在抛物线上时,坐标为(1,0),
把(1,0)代入y=2x+t,
t=2,
∴当线段GH与抛物线有两个不同的公共点,t的取值范围是![]()

【题型】解答题
【结束】
26
【题目】摇椅是老年人很好的休闲工具,右图是一张摇椅放在客厅的侧面示意图,摇椅静止时,以O为圆心OA为半径的![]() 的中点P着地,地面NP与
的中点P着地,地面NP与![]() 相切,已知∠AOB=60°,半径OA=60cm,靠背CD与OA的夹角∠ACD=127°,C为OA的中点,CD=80cm,当摇椅沿
相切,已知∠AOB=60°,半径OA=60cm,靠背CD与OA的夹角∠ACD=127°,C为OA的中点,CD=80cm,当摇椅沿![]() 滚动至点A着地时是摇椅向后的最大安全角度.
滚动至点A着地时是摇椅向后的最大安全角度.
(1)静止时靠背CD的最高点D离地面多高?
(2)静止时着地点P至少离墙壁MN的水平距离是多少时?才能使摇椅向后至最大安全角度时点D不与墙壁MN相碰.
(精确到1cm,参考数据π取3.14,sin37°=0.60,cos37°=0.80,tan37°=0.75,sin67°=0.92,cos67°=0.39,tan67°=2.36, ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E、F、G. H分别AB、BC、 CD、 DA边上的动点,且AE=BF=CG=DH

(1)求证:四边形EFGH是平行四边形:
(2)在点E、F、G、H运动过程中,判断直线GE是否经过某一定点,如果是,请你在图中画出这个点:如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B在反比例函数![]() (x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.
(x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.

(1)如图,当m=2,n=6时,直接写出点C的坐标:
(2)若A(m,n),B(n,m).连接OA、OB、AB,求△AOB的面积:(用含m的代数式表示)
(3)设AD⊥y轴于点D,BE⊥x轴于点E.若![]() ,且
,且![]() ,则当点C在直线DE上时,求p的取值范围.
,则当点C在直线DE上时,求p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了“好读书、读好书”的课外阅读活动,为了解同学们的读书情况,从全校随机抽取了![]() 名学生,并统计它们平均每天的课外阅读时间(单位:
名学生,并统计它们平均每天的课外阅读时间(单位:![]() ),然后利用所得数据绘制成如下不完整的统计图表.
),然后利用所得数据绘制成如下不完整的统计图表.
课外阅读时间频数分布表
课外阅读时间 | 频数 | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
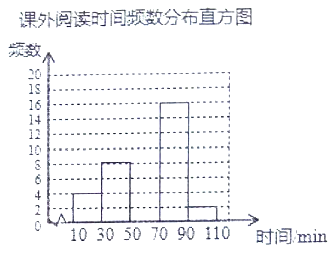
请根据图表中提供的信息回答下列问题:
(1)填空:![]() __________,
__________,![]() __________;
__________;
(2)将频数分布直方图补充完整;
(3)若全校有![]() 名学生,估计该校有多少名学生平均每天的课外阅读时间不少于
名学生,估计该校有多少名学生平均每天的课外阅读时间不少于![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点D为AB的中点,过点D作DE∥BC交AC于E.
(1)求证:E为AC的中点;
(2)如图2,过点D作QD⊥AB交BC的延长线于Q,过点E作EP⊥AC交CB的延长线于P,连AP、AQ.若PQ=12,AP+AQ=20,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com