
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)

若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
【答案】(1)加工竖式纸盒200个,加工横式纸盒400个;(2)a为:125,130,135.
【解析】试题分析:(1)根据题目可以看出一个竖式纸盒需要正方形纸片1个,长方形纸片4个,一个横式纸盒需要正方形纸片2个,长方形纸片3个,设加工竖式纸盒x个,加工横式纸盒y个,列出方程组即可;(2)本题根据题意列出方程组,得出y与a的关系式,y=40﹣![]() ,∵y、a为正整数,得出a的所有可能值.
,∵y、a为正整数,得出a的所有可能值.
试题解析:
(1) 设加工竖式纸盒x个,加工横式纸盒y个,
依题意,得![]()
解得:![]()
答:加工竖式纸盒200个,加工横式纸盒400个
(2)设加工竖式纸盒x个,加工横式纸盒y个,
依题意得:![]()
∴y=40﹣![]() ,
,
∵y、a为正整数,
∴a为5的倍数,
∵120<a<136
∴满足条件的a为:125,130,135.
当a=125时,x=20,y=15;
当a=130时,x=22,y=14;
当a=135时,x=24,y=13


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b的图象与反比例函数y2=![]() (x>0)的图象交于A、B两点,与y轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3)
(x>0)的图象交于A、B两点,与y轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3)

(1)求一次函数和反比例函数的解析式;
(2)在x轴上找一点P,使得△PAB的周长最小,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校甲乙两个体操队队员的平均身高相等,甲队队员身高的方差是S甲2=1.9,乙队队员身高的方差是S乙2=1.2,那么两队中队员身高更整齐的是队.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.

(1)求证:FD是⊙O的切线;
(2)设OC与BE相交于点G,若OG=2,求⊙O半径的长;
(3)在(2)的条件下,当OE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
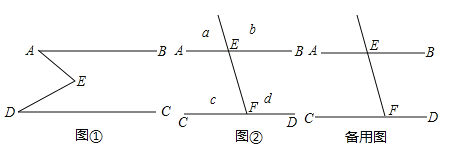
【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED= °
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1,l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com