
ΓΨΧβΡΩΓΩΕΦ‘»Ρ≥–ΘΉΦ±ΗΉι÷·―ß…ζΦΑΦ“≥Λ¥ζ±μΒΫΙπΝ÷Ϋχ––…γΜα ΒΦυΜνΕ·Θ§ΈΣ±ψ”ΎΙήάμΘ§Υυ”–»Υ‘±±Ί–κ≥ΥΉχΆ§“ΜΝ–ΗΏΧζΘ§ΗΏΧζΒΞ≥ΧΤ±ΦέΗώ»γ±μΥυ ΨΘ§ΕΰΒ»Ήυ―ß…ζΤ±Ω…¥ρ7.5’έΘ§“―÷ΣΥυ”–»Υ‘±ΕΦ¬ρ“ΜΒ»ΉυΒΞ≥ΧΜπ≥ΒΤ±–η6175‘ΣΘ§ΕΦ¬ρΕΰΒ»ΉυΒΞ≥ΧΜπ≥ΒΤ±–η3150‘ΣΘΜ»γΙϊΦ“≥Λ¥ζ±μ”κΫΧ ΠΒΡ»Υ ΐ÷°±»ΈΣ2ΘΚ1Θ°
‘Υ––«χΦδ | Τ±Φέ | ||
ΤπΒψ’Ψ | ÷’Βψ’Ψ | “ΜΒ»Ήυ | ΕΰΒ»Ήυ |
ΕΦ‘» | ΙπΝ÷ | 95Θ®‘ΣΘ© | 60Θ®‘ΣΘ© |
Θ®1Θ©≤ΈΦ”…γΜα ΒΦυΜνΕ·ΒΡάœ ΠΓΔΦ“≥Λ¥ζ±μ”κ―ß…ζΗς”–Εύ…Ό»ΥΘΩ
Θ®2Θ©”…”ΎΗς÷÷‘≠“ρΘ§ΕΰΒ»ΉυΒΞ≥ΧΜπ≥ΒΤ±÷ΜΡή¬ρx’≈Θ®xΘΦ≤ΈΦ”…γΜα ΒΦυΒΡΉή»Υ ΐΘ©Θ§Τδ”ύΒΡ–κ¬ρ“ΜΒ»ΉυΒΞ≥ΧΜπ≥ΒΤ±Θ§‘Ύ±Θ÷ΛΥυ”–»Υ‘±ΕΦ”–ΉυΈΜΒΡ«ΑΧαœ¬Θ§«κΡψ…ηΦΤΉνΨ≠ΦΟΒΡΙΚΤ±ΖΫΑΗΘ§≤Δ–¥≥ωΙΚ¬ρΒΞ≥ΧΜπ≥ΒΤ±ΒΡΉήΖ―”Οy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ°
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΖΫΑΗœ¬Θ§«κ«σ≥ωΒ±x=30 ±Θ§ΙΚ¬ρΒΞ≥ΧΜπ≥ΒΤ±ΒΡΉήΖ―”ΟΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ…η≤ΈΦ”…γΜα ΒΦυΒΡάœ Π”–m»ΥΘ§―ß…ζ”–n»ΥΘ§‘ρ―ß…ζΦ“≥Λ”–2m»ΥΘ§
ΗυΨίΧβ“βΒΟΘΚ ![]() Θ§
Θ§
ΫβΒΟΘΚ ![]() Θ§
Θ§
‘ρ2m=10Θ°
¥πΘΚ≤ΈΦ”…γΜα ΒΦυΒΡάœ ΠΓΔΦ“≥Λ”κ―ß…ζΗς”–5ΓΔ10”κ50»Υ
Θ®2Θ©ΫβΘΚ”…Θ®1Θ©÷ΣΥυ”–≤Έ”κ»Υ‘±ΉήΙ≤”–65»ΥΘ§Τδ÷–―ß…ζ”–50»ΥΘ§
ΔΌΒ±50ΓήxΘΦ65 ±Θ§ΉνΨ≠ΦΟΒΡΙΚΤ±ΖΫΑΗΈΣΘΚ
―ß…ζΕΦ¬ρ―ß…ζΤ±Ι≤50’≈Θ§Θ®x©¹50Θ©Οϊ≥…Ρξ»Υ¬ρΕΰΒ»ΉυΜπ≥ΒΤ±Θ§Θ®65©¹xΘ©Οϊ≥…Ρξ»Υ¬ρ“ΜΒ»ΉυΜπ≥ΒΤ±Θ°
ΓύΜπ≥ΒΤ±ΒΡΉήΖ―”ΟΘ®ΒΞ≥ΧΘ©y”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy=60ΓΝ0.75ΓΝ50+60Θ®x©¹50Θ©+95Θ®65©¹xΘ©Θ§
Φ¥y=©¹35x+5425Θ®50ΓήxΘΦ65Θ©ΘΜ
ΔΎΒ±0ΘΦxΘΦ50 ±Θ§ΉνΨ≠ΦΟΒΡΙΚΤ±ΖΫΑΗΈΣΘΚ“Μ≤ΩΖ÷―ß…ζ¬ρ―ß…ζΤ±Ι≤x’≈Θ§Τδ”ύΒΡ―ß…ζ”κΦ“≥Λάœ Π“ΜΤπΙΚ¬ρ“ΜΒ»ΉυΜπ≥ΒΤ±Ι≤Θ®65©¹xΘ©’≈Θ°
ΓύΜπ≥ΒΤ±ΒΡΉήΖ―”ΟΘ®ΒΞ≥ΧΘ©y”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy=60ΓΝ0.75x+95Θ®65©¹xΘ©Θ§
Φ¥y=©¹50x+6175Θ®0ΘΦxΘΦ50Θ©
ΓύΙΚ¬ρΒΞ≥ΧΜπ≥ΒΤ±ΒΡΉήΖ―”Οy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy= ![]()
Θ®3Θ©ΫβΘΚΓΏx=30ΘΦ50Θ§
Γύy=©¹50x+6175=©¹50ΓΝ30+6185=4675Θ§
¥πΘΚΒ±x=30 ±Θ§ΙΚ¬ρΒΞ≥ΧΜπ≥ΒΤ±ΒΡΉήΖ―”ΟΈΣ4675‘Σ
ΓΨΫβΈωΓΩΘ®1Θ©…η≤ΈΦ”…γΜα ΒΦυΒΡάœ Π”–m»ΥΘ§―ß…ζ”–n»ΥΘ§‘ρ―ß…ζΦ“≥Λ”–2m»ΥΘ§»τΕΦ¬ρΕΰΒ»ΉυΒΞ≥ΧΜπ≥ΒΤ±«“Μ®«°Ήν…ΌΘ§‘ρ»ΪΧε―ß…ζΕΦ–η¬ρΕΰΒ»Ήυ―ß…ζΤ±Θ§ΗυΨίΧβ“βΒΟΒΫΖΫ≥ΧΉιΘ§«σ≥ωΖΫ≥ΧΉιΒΡΫβΦ¥Ω…ΘΜΘ®2Θ©”–ΝΫ÷÷«ιΩωΘΚΔΌΒ±50ΓήxΘΦ65 ±Θ§―ß…ζΕΦ¬ρ―ß…ζΤ±Ι≤50’≈Θ§Θ®x©¹50Θ©Οϊ≥…Ρξ»Υ¬ρΕΰΒ»ΉυΜπ≥ΒΤ±Θ§Θ®65©¹xΘ©Οϊ≥…Ρξ»Υ¬ρ“ΜΒ»ΉυΜπ≥ΒΤ±Θ§ΒΟΒΫΫβΈω ΫΘΚy=60ΓΝ0.75ΓΝ50+60Θ®x©¹50Θ©+95Θ®65©¹xΘ©ΘΜΔΎΒ±0ΘΦxΘΦ50 ±Θ§“Μ≤ΩΖ÷―ß…ζ¬ρ―ß…ζΤ±Ι≤x’≈Θ§Τδ”ύΒΡ―ß…ζ”κΦ“≥Λάœ Π“ΜΤπΙΚ¬ρ“ΜΒ»ΉυΜπ≥ΒΤ±Ι≤Θ®65©¹xΘ©’≈Θ§ΒΟΒΫΫβΈω Ϋ «y=©¹50x+6175ΘΜΘ®3Θ©”…Θ®2Θ©–ΓΧβ÷ΣΘΚΒ±x=30 ±Θ§y=©¹50x+6175Θ§¥ζ»κ«σΫβΦ¥Ω…«σΒΟ¥πΑΗΘ°¥ΥΧβΩΦ≤ιΝΥ“Μ¥ΈΚ· ΐΒΡ ΒΦ ”Π”ΟΘ°ΫβΨω±ΨΧβΒΡΙΊΦϋ «Ζ÷ΕΈΚ· ΐΒΡ‘Υ”ΟΘ§Κ· ΐΒΡΉν÷ΒΘ°ΩΦ≤ι―ß…ζΖ÷ΈωΫβΨωΈ ΧβΒΡΡήΝΠΘ§ τ”Ύ÷–ΒΒΧβΘ°


 –¬ΩΈ±ξΫΉΧί‘ΡΕΝ―ΒΝΖœΒΝ–¥πΑΗ
–¬ΩΈ±ξΫΉΧί‘ΡΕΝ―ΒΝΖœΒΝ–¥πΑΗ ΩΎΥψ–ΡΥψΥΌΥψ”Π”ΟΧβœΒΝ–¥πΑΗ
ΩΎΥψ–ΡΥψΥΌΥψ”Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψM «œΏΕΈAB÷–ΒψΘ§ADΓΔBCΫΜ”ΎΒψNΘ§Ν§Ϋ”ACΓΔBDΓΔMCΓΔMDΘ§Γœl=Γœ2Θ§Γœ3=Γœ4Θ°
Θ®1Θ©«σ÷ΛΘΚΓςAMDΓ’ΓςBMCΘΜ
Θ®2Θ©ΆΦ÷–‘Ύ≤ΜΧμΦ”–¬ΒΡΉ÷ΡΗΒΡ«ιΩωœ¬Θ§«κ–¥≥ω≥ΐΝΥΓΑΓςAMDΓ’ΓςBMCΓ±“‘ΆβΒΡΥυ”–»ΪΒ»»ΐΫ«–ΈΘ§≤Δ―Γ≥ωΤδ÷–“ΜΕ‘Ϋχ––÷ΛΟςΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§±Ώ≥ΛΖ÷±πΈΣ1ΚΆ2ΒΡΝΫΗωΒ»±Ώ»ΐΫ«–ΈΘ§ΩΣ ΦΥϋΟ«‘ΎΉσ±Ώ÷ΊΚœΘ§¥σ»ΐΫ«–ΈΙΧΕ®≤ΜΕ·Θ§»ΜΚσΑ―–Γ»ΐΫ«–ΈΉ‘Ήσœρ”“ΤΫ“Τ÷±÷Ν“Τ≥ω¥σ»ΐΫ«–ΈΆβΆΘ÷ΙΘ°…η–Γ»ΐΫ«–Έ“ΤΕ·ΒΡΨύάκΈΣxΘ§ΝΫΗω»ΐΫ«–Έ÷ΊΒΰΟφΜΐΈΣyΘ§‘ρyΙΊ”ΎxΒΡΚ· ΐΆΦœσ «Θ® Θ©
A.
B.
C.
D.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΖΫΗώ÷Ϋ÷–ΟΩΗω–ΓΖΫΗώΕΦΒΡ±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈΘ§Έ“Ο«Α―“‘ΗώΒψΝ§œΏΈΣ±ΏΒΡΕύ±Ώ–Έ≥ΤΈΣΓΑΗώΒψΕύ±Ώ–ΈΓ±Θ°

Θ®1Θ©‘ΎΆΦ1÷–»ΖΕ®ΗώΒψDΘ§≤ΔΜ≠≥ω“ΜΗω“‘AΓΔBΓΔCΓΔDΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΘ§ ΙΤδΈΣ÷αΕ‘≥ΤΆΦ–ΈΘΜ
Θ®2Θ©‘ΎΆΦ2÷–Μ≠“ΜΗωΗώΒψ’ΐΖΫ–ΈΘ§ ΙΤδΟφΜΐΒ»”Ύ10ΘΜ
Θ®3Θ©÷±Ϋ”–¥≥ωΆΦ3÷–ΓςFGHΒΡΟφΜΐ «ΓΓΓΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§ΒψD « ![]() …œ“ΜΒψΘ§«“ΓœBDE=ΓœCBEΘ§BD”κAEΫΜ”ΎΒψFΘ°
…œ“ΜΒψΘ§«“ΓœBDE=ΓœCBEΘ§BD”κAEΫΜ”ΎΒψFΘ° 
Θ®1Θ©«σ÷ΛΘΚBC «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τBDΤΫΖ÷ΓœABEΘ§«σ÷ΛΘΚDE2=DFDBΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§―”≥ΛEDΓΔBAΫΜ”ΎΒψPΘ§»τPA=AOΘ§DE=2Θ§«σPDΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§ΗΏ
Θ§ΗΏ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ÷ή≥Λ «Θ® Θ©Θ°
ΒΡ÷ή≥Λ «Θ® Θ©Θ°
A. 42 B. 32 C. 37Μρ33 D. 42Μρ32
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Β»―ϋ÷±Ϋ«ΓςABC÷–Θ§ΓœBAC=90ΓψΘ§BC=6Θ§ΙΐΒψCΉςCDΓΆBCΘ§CD=2Θ§Ν§Ϋ”BDΘ§ΙΐΒψCΉςCEΓΆBDΘ§¥ΙΉψΈΣEΘ§Ν§Ϋ”AEΘ§‘ρAE≥ΛΈΣ_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–«ΤΎΝυ‘γ≥Ω»ο»ο¬η¬η¥”Φ“άο≥ωΖΔ»ΞΙέ…ΫΚΰΙΪ‘ΑΕΆΝΕΘ§ΥΐΝ§–χΓΔ‘»ΥΌΉΏΝΥ60minΚσΜΊΦ“Θ§ΆΦ÷–ΒΡ’έœΏΕΈOA©¹AB©¹BC «Υΐ≥ωΖΔΚσΥυ‘ΎΈΜ÷ΟάκΦ“ΒΡΨύάκsΘ®kmΘ©”κ––ΉΏ ±ΦδtΘ®minΘ©÷°ΦδΒΡΚ· ΐΙΊœΒΘ§‘ρœ¬Ν–ΆΦ–Έ÷–Ω…“‘¥σ÷¬Οη ω»ο»ο¬η¬η––ΉΏΒΡ¬ΖœΏ «Θ® Θ© 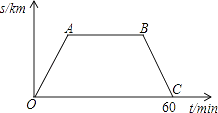
A.
B.
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏLΘΚy=ax2+bx+c”κx÷αΫΜ”ΎAΓΔBΘ®3Θ§0Θ©ΝΫΒψΘ®A‘ΎBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ®0Θ§3Θ©Θ§“―÷ΣΕ‘≥Τ÷αx=1Θ°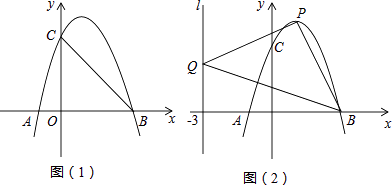
Θ®1Θ©«σ≈ΉΈοœΏLΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΫΪ≈ΉΈοœΏLœρœ¬ΤΫ“ΤhΗωΒΞΈΜ≥ΛΕ»Θ§ ΙΤΫ“ΤΚσΥυΒΟ≈ΉΈοœΏΒΡΕΞΒψ¬δ‘ΎΓςOBCΡΎΘ®Αϋά®ΓςOBCΒΡ±ΏΫγΘ©Θ§«σhΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©…ηΒψP «≈ΉΈοœΏL…œ»Έ“ΜΒψΘ§ΒψQ‘Ύ÷±œΏlΘΚx=©¹3…œΘ§ΓςPBQΡήΖώ≥…ΈΣ“‘ΒψPΈΣ÷±Ϋ«ΕΞΒψΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τΡήΘ§«σ≥ωΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com