
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.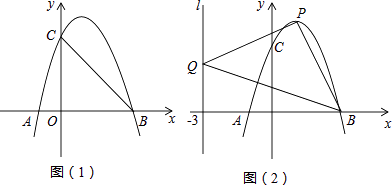
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
【答案】
(1)
解:∵抛物线的对称轴x=1,B(3,0),
∴A(﹣1,0)
∵抛物线y=ax2+bx+c过点C(0,3)
∴当x=0时,c=3.
又∵抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0)
∴ ![]() ,
,
∴ ![]()
∴抛物线的解析式为:y=﹣x2+2x+3
(2)
解:∵C(0,3),B(3,0),
∴直线BC解析式为y=﹣x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4)
∵对于直线BC:y=﹣x+1,当x=1时,y=2;将抛物线L向下平移h个单位长度,
∴当h=2时,抛物线顶点落在BC上;
当h=4时,抛物线顶点落在OB上,
∴将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),
则2≤h≤4
(3)
解:设P(m,﹣m2+2m+3),Q(﹣3,n),
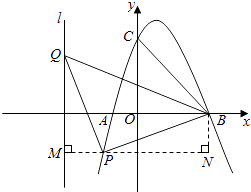
①当P点在x轴上方时,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,如图所示:
∵B(3,0),
∵△PBQ是以点P为直角顶点的等腰直角三角形,
∴∠BPQ=90°,BP=PQ,
则∠PMQ=∠BNP=90°,∠MPQ=∠NBP,
在△PQM和△BPN中, 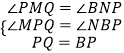 ,
,
∴△PQM≌△BPN(AAS),
∴PM=BN,
∵PM=BN=﹣m2+2m+3,根据B点坐标可得PN=3﹣m,且PM+PN=6,
∴﹣m2+2m+3+3﹣m=6,
解得:m=1或m=0,
∴P(1,4)或P(0,3).
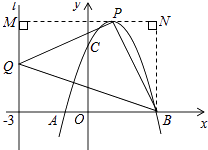
②当P点在x轴下方时,过P点作PM垂直于l于M点,过B点作BN垂直于MP的延长线与N点,
同理可得△PQM≌△BPN,
∴PM=BN,
∴PM=6﹣(3﹣m)=3+m,BN=m2﹣2m﹣3,
则3+m=m2﹣2m﹣3,
解得m= ![]() 或
或 ![]() .
.
∴P( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
综上可得,符合条件的点P的坐标是(1,4),(0,3),( ![]() ,
, ![]() )和(
)和( ![]() ,
, ![]() ).
).
【解析】(1)利用待定系数法求出抛物线的解析式即可;(2)先求出直线BC解析式为y=﹣x+3,再求出抛物线顶点坐标,得出当x=1时,y=2;结合抛物线顶点坐即可得出结果;(3)设P(m,﹣m2+2m+3),Q(﹣3,n),由勾股定理得出PB2=(m﹣3)2+(﹣m2+2m+3)2 , PQ2=(m+3)2+(﹣m2+2m+3﹣n)2 , BQ2=n2+36,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,由AAS证明△PQM≌△BPN,得出MQ=NP,PM=BN,则MQ=﹣m2+2m+3﹣n,PN=3﹣m,得出方程﹣m2+2m+3﹣n=3﹣m,解方程即可.本题是二次函数综合题目,考查了用待定系数法求出抛物线的解析式、抛物线的顶点式、等腰直角三角形的性质、全等三角形的判定与性质、坐标与图形性质等知识;本题综合性强,有一定难度,特别是(3)中,需要通过作辅助线证明三角形全等才能得出结果.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为2:1.
运行区间 | 票价 | ||
起点站 | 终点站 | 一等座 | 二等座 |
都匀 | 桂林 | 95(元) | 60(元) |
(1)参加社会实践活动的老师、家长代表与学生各有多少人?
(2)由于各种原因,二等座单程火车票只能买x张(x<参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用y与x之间的函数关系式.
(3)在(2)的方案下,请求出当x=30时,购买单程火车票的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△AOB的顶点O在直线l上,且AO=AB.

(1)画出△AOB关于直线l成轴对称的图形△COD,且使点A的对称点为点C ;
(2)在(1)的条件下,AC与BD的位置关系是________;
(3)在(1)、(2)的条件下,联结AD,如果∠ABD=2∠ADB,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学校图书馆上个月借阅情况,管理老师从学生对艺术、经济、科普及生活四类图书借阅情况进行了统计,并绘制了下列不完整的统计图,请根据图中信息解答下列问题: 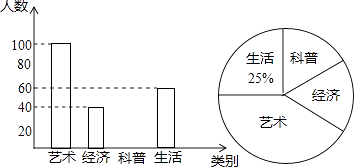
(1)上个月借阅图书的学生有多少人?扇形统计图中“艺术”部分的圆心角度数是多少?
(2)把条形统计图补充完整;
(3)从借阅情况分析,如果要添置这四类图书300册,请你估算“科普”类图书应添置多少册合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF. 
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF , 求BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,若点P能落在线段AB上,则线段CF长的最小值是_____.
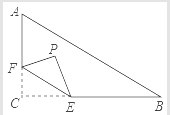
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com