
分析 根据大于零的数是正数,小于零的数是负数,有限小数或无限循环小数是有理数,无限不循环小数是无理数,可得答案.
解答 解:(1)正数集合:{ 1,$\frac{π}{2}$,$\frac{22}{7}$};
(2)负数集合:{-1.2,-1.010010001,-0.$\stackrel{•}{0}$$\stackrel{•}{2}$};
(3)有理数集合:{-1.2,0,1,$\frac{22}{7}$,-0.$\stackrel{•}{0}$$\stackrel{•}{2}$};
(4)无理数集合:{ $\frac{π}{2}$,-1.010010001…};
故答案为:1,$\frac{π}{2}$,$\frac{22}{7}$;-1.2,-1.010010001,-0.$\stackrel{•}{0}$$\stackrel{•}{2}$;-1.2,0,1,$\frac{22}{7}$,-0.$\stackrel{•}{0}$$\stackrel{•}{2}$;$\frac{π}{2}$,-1.010010001….
点评 此题主要考查了实数,实数包括有理数和无理数;实数可分为正数、负数和0.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
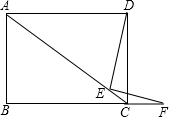 如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.
如图:四边形ABCD为矩形,E在对角线AC上,F在边BC的延长线上,且$\frac{DE}{EF}$=$\frac{BC}{AB}$,求证:DE⊥EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 桌子张数 | 4 | 5 | … | n |
| 可坐人数 | 12 | 14 | … | 4+2n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
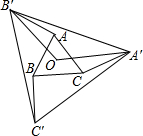 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com