
【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点坐标为A(1,-4),B(5,-4),C(4,-1).

(1)在方格纸中画出△ABC;
(2)求出△ABC的面积;
(3)若把△ABC向上平移6个单位长度,再向左平移7个单位长度得到△A′B′C′,在图中画出△A′B′C′,并写出B′的坐标.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知AD=BC,AB=DC,试判断∠A与∠B的关系,下面是小颖同学的推导过程,你能说明小颖的每一步的理由吗?

解:连接BD
在△ABD与△CDB中
AD=BC(______)
AB=CD(______)
BD=DB(______)
∴△ABD≌△CDB(______)
∴∠ADB=∠CBD(______)
∴AD∥BC(______)
∴∠A+∠ABC=180°(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考查学生的综合素质,九年级毕业生统一参加理化生实践操作科目考试。根据我市实际情况,市教育局决定:理化生实践考查科目命制24题,分4个试题单元,每个单元内含6道理化生实验操作题。即:物理3题;化学2题;生物1题。小聪与小明是某实验中学九年级的同班同学,在三月份举行的理化生考试中,他们同时抽到同一个试题单元,且每个同学都是同一个试题单元里随机抽取一题。
(1)小聪抽到物理学科科目可能性有多大?
(2)用列表法或树状图,求他俩同时抽到生物的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课堂探究性活动蔚然成风。张老师在课堂上设置一道习题:
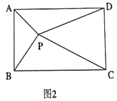
(1)已知矩形ABCD和点P,当点P在BC上任一位置(如图1所示)时,探究PA2、PB2、PC2、PD2,之间的关系?直接写出结论,不必证明;
当P点在其它位置时,请同学们分组探究:
(2)当点P在矩形内部,如图2时,探究PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论写出来,并给予证明。
(3)当点P在矩形外部,如图3时,继续探完PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论直接写出来,不必证明。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)8+(-![]() )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|-![]() |÷(
|÷(![]() -
-![]() )×(-4)2.
)×(-4)2.
(3)(![]() -
-![]() +
+![]() )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-![]() )÷3×[2-(-3)2].
)÷3×[2-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数
2 -4 8 -16 32 -64 ……
4 -2 10 -24 34 -62 ……
-1 5 -7 17 -31 65 ……
(1)第一行第7个数为
(2)第③行中是否存在连续的三个数使得三个数的和为768?若存在,求出这三个数;不存在,则说明理由;
(3)是否存在这样的一列,使得其中的三个数的和为1282?若存在,则求出这三个数,不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
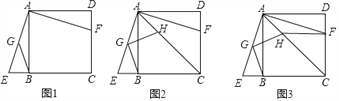
【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2![]() ,求线段HF的长.
,求线段HF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com