
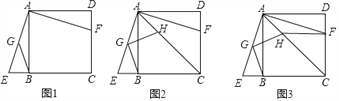
【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2![]() ,求线段HF的长.
,求线段HF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)5.
【解析】试题分析:(1)如图1中,由△ABE≌△ADF,推出∠AFD=∠E,由AG=GE,推出GB=GE=GA,推出∠E=∠GBE=∠AFD,由∠GBE+∠GBC=180°,推出∠AFD+∠GBC=180°即可;
(2)如图2中,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK.只要证明O、H、G、B四点共圆,由AG=GE,AO=OC.推出OG∥CE,推出∠GOB=∠OBC=45°,即可解决问题;
(3)如图3中,如图3中,设OG交AB于T,GH交AB于P.,作HM⊥DF于M.只要证明∠EAB=∠GBP=∠PGT=∠HBO,推出tan∠EAB=tan∠HBO=![]() ,由CH=3AH,OA=OC=OB,推出tan∠EAB=tan∠HBO=
,由CH=3AH,OA=OC=OB,推出tan∠EAB=tan∠HBO=![]() =
=![]() ,BE=DF=
,BE=DF=![]() ,在RtHMF中,利用勾股定理即可解决问题.
,在RtHMF中,利用勾股定理即可解决问题.
试题解析:(1)如图1,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠AEF=90°,
∴∠EAB=∠DAF,∵∠ABE=∠ADF=90°,∴△ABE≌△ADF,∴∠AFD=∠E,
∵AG=GE,∴GB=GE=GA,∴∠E=∠GBE=∠AFD,∵∠GBE+∠GBC=180°,∴∠AFD+∠GBC=180°;
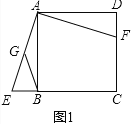
(2)如图2,连接BD交AC于O,连接OG、BH、取BH的中点K,连接GK、OK,
∵∠BGH=∠BOH=90°,BK=KH,∴GK=KH=OK=KB,∴O、H、G、B四点共圆,
∵AG=GE,AO=OC,∴OG∥CE,
∴∠GOB=∠OBC=45°,∴∠GOH=∠GBH=45°,∵∠BGH=90°,
∴∠GBH=∠GHB=45°, ∴GH=GB;
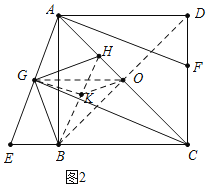
(3)如图3,设OG交AB于T,GH交AB于P,作HM⊥DF于M,
∵OG∥EC,AB⊥CE,∴OG⊥AB,易证∠EAB=∠GBP=∠PGT=∠HBO,
∴tan∠EAB=tan∠HBO=![]() ,∵CH=3AH,OA=OC=OB,∴tan∠EAB=tan∠HBO=
,∵CH=3AH,OA=OC=OB,∴tan∠EAB=tan∠HBO=![]() =
=![]() ,
,
∵AB=AD=2![]() ,∴BE=DF=
,∴BE=DF=![]() ,在Rt△HMF中,易证FM=
,在Rt△HMF中,易证FM=![]() ,HM=
,HM=![]() ,
,
∴HF=![]() =5.
=5.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式![]() 成立的一对有理数“
成立的一对有理数“![]() ,
,![]() ”为“共生有理数对”,记为(
”为“共生有理数对”,记为(![]() ,
,![]() ).
).
(1)通过计算判断数对“2,1,“4,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“n,m”___“共生有理数对”(填“是”或“不是”),并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点坐标为A(1,-4),B(5,-4),C(4,-1).

(1)在方格纸中画出△ABC;
(2)求出△ABC的面积;
(3)若把△ABC向上平移6个单位长度,再向左平移7个单位长度得到△A′B′C′,在图中画出△A′B′C′,并写出B′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
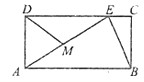
【题目】如图,在矩形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 上一点,且
上一点,且![]() ,
, ![]() 为
为![]() 的中点.下列结论:①
的中点.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有____________.(请把所有正确结论的序号填在横线上)
.其中正确的有____________.(请把所有正确结论的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
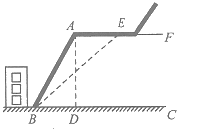
【题目】今年夏季山洪暴发,易发生滑坡,经过地质人员勘测,当坡角不超过![]() 时,可以确保山体不滑坡.某中学紧挨一座山体斜坡,如图所示,已知
时,可以确保山体不滑坡.某中学紧挨一座山体斜坡,如图所示,已知![]() ,斜坡
,斜坡![]() 长30米,坡角
长30米,坡角![]() ,为保证改造后的山体不滑坡,求
,为保证改造后的山体不滑坡,求![]() 至少是多少米?(精确到0.1米,
至少是多少米?(精确到0.1米, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国西部地区约占我国国土面积的![]() ,我国国土面积约960万平方公里。若用科学记数法表示,则我国西部地区的面积为( )
,我国国土面积约960万平方公里。若用科学记数法表示,则我国西部地区的面积为( )
A. 6.4×106平方公里 B. 6.4×107平方公里
C. 640×104平方公里 D. 64×105平方公里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学活动小组在做角的拓展图形练习时,经历了如下过程:

(1)操作发现:点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,如图:将图1中的三角板绕点
的下方,如图:将图1中的三角板绕点![]() 旋转,当直角三角板的
旋转,当直角三角板的![]() 边在
边在![]() 的内部,且恰好平分
的内部,且恰好平分![]() 时,如图2.则下列结论正确的是 (填序号即可).
时,如图2.则下列结论正确的是 (填序号即可).
①![]() ②
②![]() ③
③![]() 平分
平分![]() ④
④![]() 的平分线在直线
的平分线在直线![]() 上
上
(2)数学思考:同学们在操作中发现,当三角板绕点![]() 旋转时,如果直角三角板的
旋转时,如果直角三角板的![]() 边在
边在![]() 的内部且另一边
的内部且另一边![]() 在直线AB的下方,那么
在直线AB的下方,那么![]() 与
与![]() 的差不变,请你说明理由;如果直角三角板的
的差不变,请你说明理由;如果直角三角板的![]() 、
、![]() 边都在
边都在![]() 的内部,那么
的内部,那么![]() 与
与![]() 的和不变,请直接写出
的和不变,请直接写出![]() 与
与![]() 的和,不要求说明理由.
的和,不要求说明理由.
(3)类比探索:三角板绕点![]() 继续旋转,当直角三角板的
继续旋转,当直角三角板的![]() 边在
边在![]() 的内部时,如图3,求
的内部时,如图3,求![]() 与
与![]() 相差多少度?为什么?
相差多少度?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下列要求画图,并回答问题.
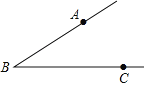
如图,已知∠ABC.
(1)在射线BC上戳取BD=BA,连接AD;
(2)画∠ABD的平分线交线段AD于点M.
回答问题:线段AM和线段DM的大小关系是:AM DM.∠AMB的度数为 度.(精确到1度).
(友情提醒:截取用圆规,并保留痕迹:画完图要下结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com