
【题目】阅读材料后解决问题:
计算:(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据以上解决问题的方法,试着解决:
(3+1)(32+1)(34+1)(38+1)…(364+1)=__
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() , 求AE的长.
, 求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() , sinA=
, sinA=![]() , 求PC的长.
, 求PC的长.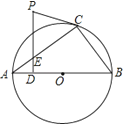
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC。

(1)若D为AC的中点,BD把三角形的周长分为24cm和30cm两部分,求△ABC三边的长;
(2)若D为AC上一点,试说明AC>![]() (BD+DC)。
(BD+DC)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y= ![]() x﹣2
x﹣2
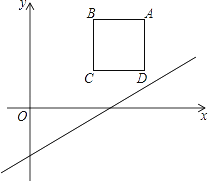
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
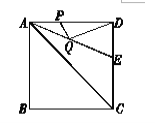
【题目】如图,正方形ABCD的边长是4, ![]() 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则![]() 的最小值是( )
的最小值是( )
A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.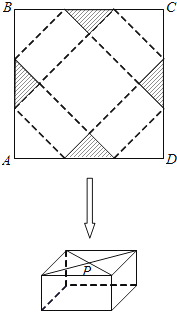
(1)若折叠后长方体底面正方形的面积为1250cm2 , 求长方体包装盒的高;
(2)设剪掉的等腰直角三角形的直角边长为x(cm),长方体的侧面积为S(cm2),求S与x的函数关系式,并求x为何值时,S的值最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com