
【题目】如图,正方形ABCD的边长是4, ![]() 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则![]() 的最小值是( )
的最小值是( )
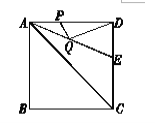
A. 2 B. 4 C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】阅读材料后解决问题:
计算:(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
(2+1)(22+1)(24+1)(28+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据以上解决问题的方法,试着解决:
(3+1)(32+1)(34+1)(38+1)…(364+1)=__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,平面直角坐标系xOy中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线y=-![]() x+b交折线O-A-B于点E.
x+b交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与b的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B﹣C﹣D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 若AP=BP,则点P是线段的中点 B. 若点C在线段AB上,则AB=AC+BC
C. 若AC+BC>AB,则点C一定在线段AB外 D. 两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考体育测试,其中男生测试项目有1000米跑、立定跳远、掷实心球、一分钟跳绳、引体向上五个项目.考生须从这五个项目中选取三个项目,要求:1000米跑必选,立定跳远和掷实心球二选一,一分钟跳绳和引体向上二选一.
(1)写出男生在体育测试中所有可能选择的结果;
(2)请你用列表法或画树状图法,求出两名男生在体育测试中所选项目完全相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有如图所示的一块地,已知AD=4米,CD=3米,![]() ,AB=13米,BC=12米.
,AB=13米,BC=12米.
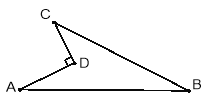
(1)试判断以点A、点B、点C为顶点的三角形是什么三角形?并说明理由.
(2)求这块地的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com