练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列说法错误的是（ ）

    A. 若AP=BP,则点P是线段的中点 B. 若点C在线段AB上，则AB=AC+BC

    C. 若AC+BC>AB,则点C一定在线段AB外 D. 两点之间，线段最短

    【答案】A

    【解析】

    根据线段中点的定义、线段的和差、线段的性质逐项进行判断即可得.

    A、如果点P不在线段AB上，如图所示，此时AP=BP，但是点P不是线段AB的中点，原说法错误，故本选项符合题意；

    B、若点C在线段AB上，则AB=AC+BC，原说法正确，故本选项不符合题意；

    C、若AC+BC＞AB，则点C不可能在线段AB上，因为如果点C在线段AB上，那么AC+BC=AB，与已知条件AC+BC＞AB矛盾，则点C一定在线段AB外，原说法正确，故本选项不符合题意；

    D、两点之间，线段最短，原说法正确，故本选项不符合题意，

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC内接于⊙O，AB是⊙O的直径．PC是⊙O的切线，C为切点，PD⊥AB于点D，交AC于点E．
    （1）求证：∠PCE=∠PEC；
    （2）若AB=10，ED= ， sinA= ， 求PC的长．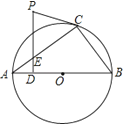

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初二学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

    （1）在这次评价中，一共抽查了 名学生；

    （2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为 度；

    （3）请将频数分布直方图补充完整；

    （4）如果全市有6000名初二学生，那么在试卷评讲课中，“独立思考”的初二学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长是4， 的平分线交DC于点E．若点P，Q分别是AD和AE上的动点，则的最小值是（　　）

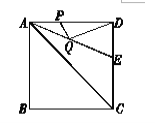
    A. 2 B. 4 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把一个棱长为的正方体的每个面等分成个小正方形，然后沿每个面正中心的一个正方形向里挖空（相当于挖去个小正方体），所得到的几何体的表面积是（ ）

    A. 78 B. 72 C. 54 D. 48

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，O为坐标原点．已知反比例函数y=（k＞0）的图象经过点A（2，m），过点A作AB⊥x轴于点B，且△AOB的面积为．

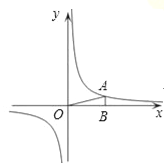
    （1）求k和m的值；

    （2）点C（x，y）在反比例函数y=的图象上，求当1≤x≤3时函数值y的取值范围；

    （3）过原点O的直线l与反比例函数y=的图象交于P、Q两点，试根据图象直接写出线段PQ长度的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

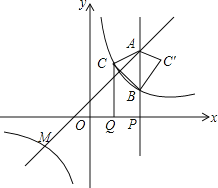
    【题目】如图，点M（－3，m）是函数y＝x＋1与反比例函数（k≠0）的图象的一个交点．

    （1）求反比例函数表达式；

    （2）点P是x轴正半轴上的一个动点，设OP＝a（a≠2），过点P作垂直于x轴的直线，分别交一次函数，反比例函数的图象于点A，B，过OP的中点Q作x轴的垂线，交反比例函数的图象于点C，△ABC′与△ABC关于直线AB对称．

    ①当a＝4时，求△ABC′的面积；

    ②若△AMC与△AMC′的面积相等，求a的值 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是边长为60cm的正方形硬纸片，剪掉阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使A、B、C、D四个点重合于图中的点P，正好形成一个底面是正方形的长方体包装盒．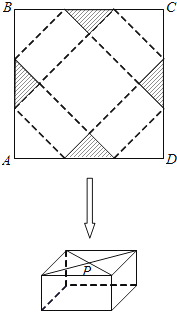

    （1）若折叠后长方体底面正方形的面积为1250cm2 ， 求长方体包装盒的高；
    （2）设剪掉的等腰直角三角形的直角边长为x（cm），长方体的侧面积为S（cm2），求S与x的函数关系式，并求x为何值时，S的值最大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A，C的坐标分别为A（10，0），C（0，4），点D是OA的中点，点P为线段BC上的点．小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标（3，4），请你写出其余所有符合这个条件的P点坐标　 　．

    查看答案和解析>>

    同步练习册答案