
【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为![]() .
.
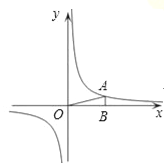
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=![]() 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
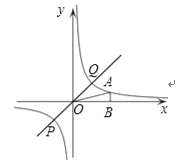
(3)过原点O的直线l与反比例函数y=![]() 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
【答案】(1)m=![]() k=1(2)
k=1(2)![]() ≤y≤1(3)2
≤y≤1(3)2![]()
【解析】试题分析:(1)根据三角形的面积公式先得到m的值,然后把点A的坐标代入y=![]() ,可求出k的值;
,可求出k的值;
(2)根据反比例函数得性质求解;
(3)P,Q关于原点对称,则PQ=2OP,设P(a,![]() ),根据勾股定理得到OP=
),根据勾股定理得到OP=![]() ,从而得到OP最小值为
,从而得到OP最小值为![]() ,于是可得到线段PQ长度的最小值.
,于是可得到线段PQ长度的最小值.
试题解析:(1)∵A(2,m),
∴OB=2,AB=m,
∴S△AOB=![]() OBAB=
OBAB=![]() ×2×m=
×2×m=![]() ,
,
∴m=![]() ;
;
∴点A的坐标为(2,![]() ),
),
把A(2,![]() )代入y=
)代入y=![]() ,得
,得![]() ,
,
∴k=1;
(2)∵当x=1时,y=1;当x=3时,y=![]() ,
,
又∵反比例函数y=![]() ,在x>0时,y随x的增大而减小,
,在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为![]() ≤y≤1;
≤y≤1;
(3)由图象可得:P,Q关于原点对称,
∴PQ=2OP,
反比例函数解析式为y=![]() ,设P(a,
,设P(a,![]() ),
),
∴OP=![]() ,
,
∴OP最小值为![]() ,
,
∴线段PQ长度的最小值为2![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.
光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.
(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线;
(2)当⊙O的半径为1时,如图3,
①第一象限内的一条入射光线平行于x轴,且自⊙O的外部照射在其上点P处,此光线经⊙O反射后,反射光线与y轴平行,则反射光线与切线l的夹角为;
②自点A(﹣1,0)出发的入射光线,在⊙O内不断地反射.若第1个反射点P1在第二象限,且第12个反射点P12与点A重合,则第1个反射点P1的坐标为
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.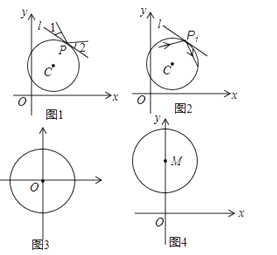
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠B=30°.动点P从点B出发,沿B﹣C﹣D的路线向点D运动.设△ABP的面积为y(B、P两点重合时,△ABP的面积可以看做0),点P运动的路程为x,则y与x之间函数关系的图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 若AP=BP,则点P是线段的中点 B. 若点C在线段AB上,则AB=AC+BC
C. 若AC+BC>AB,则点C一定在线段AB外 D. 两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1)、B(﹣1,1)、C(0,﹣2).
(1)点B关于坐标原点O对称的点的坐标为;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B1的反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考体育测试,其中男生测试项目有1000米跑、立定跳远、掷实心球、一分钟跳绳、引体向上五个项目.考生须从这五个项目中选取三个项目,要求:1000米跑必选,立定跳远和掷实心球二选一,一分钟跳绳和引体向上二选一.
(1)写出男生在体育测试中所有可能选择的结果;
(2)请你用列表法或画树状图法,求出两名男生在体育测试中所选项目完全相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰梯形OABC在平面直角坐标系中,如图A(1,2),B(3,2),C(4,0),则过点M(0,5)且把等腰梯形OABC面积分成相等两部分的直线解析式是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com