
【题目】某市今年中考体育测试,其中男生测试项目有1000米跑、立定跳远、掷实心球、一分钟跳绳、引体向上五个项目.考生须从这五个项目中选取三个项目,要求:1000米跑必选,立定跳远和掷实心球二选一,一分钟跳绳和引体向上二选一.
(1)写出男生在体育测试中所有可能选择的结果;
(2)请你用列表法或画树状图法,求出两名男生在体育测试中所选项目完全相同的概率.
【答案】
(1)
解:将立定跳远、掷实心球、一分钟跳绳和引体向上分别用A,B,C,D表示,
画树状图得:
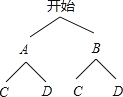
可得可能选择的结果有四种:①1000米跑、立定跳远、一分钟跳绳;②1000米跑、立定跳远、引体向上;③1000米跑、掷实心球、一分钟跳绳;④1000米跑、掷实心球、引体向上;
(2)
解:列表得
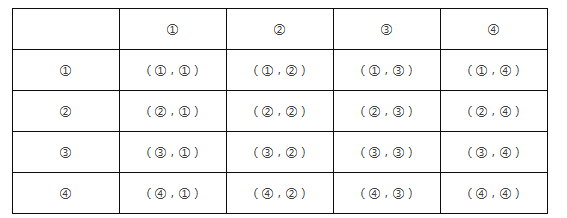
∵所有可能出现的结果共有16种,其中所选项目相同的有4种.
∴两人所选项目相同的概率为: ![]()
【解析】(1)首先将立定跳远、掷实心球、一分钟跳绳和引体向上分别用A,B,C,D表示,然后画树状图,由树状图求得所有等可能的结果;(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与两名男生在体育测试中所选项目完全相同的情况,再利用概率公式求解即可求得答案.
【考点精析】根据题目的已知条件,利用列表法与树状图法的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
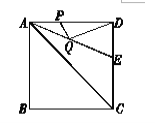
【题目】如图,正方形ABCD的边长是4, ![]() 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则![]() 的最小值是( )
的最小值是( )
A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
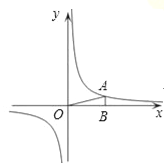
【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=![]() 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y=![]() 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
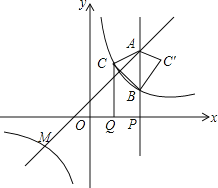
【题目】如图,点M(-3,m)是函数y=x+1与反比例函数![]() (k≠0)的图象的一个交点.
(k≠0)的图象的一个交点.
(1)求反比例函数表达式;
(2)点P是x轴正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.
①当a=4时,求△ABC′的面积;
②若△AMC与△AMC′的面积相等,求a的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A. 两条对角线相等的四边形是矩形;
B. 有一条对角线平分一个内角的平行四边形为菱形;
C. 对角线互相垂直且相等的四边形是正方形;
D. 依次连结四边形各边的中点,所得四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.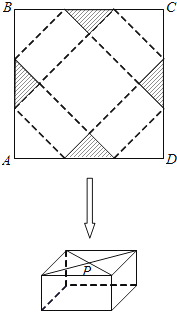
(1)若折叠后长方体底面正方形的面积为1250cm2 , 求长方体包装盒的高;
(2)设剪掉的等腰直角三角形的直角边长为x(cm),长方体的侧面积为S(cm2),求S与x的函数关系式,并求x为何值时,S的值最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com