
����Ŀ����ͼ����M����3��m���Ǻ���y��x��1�뷴��������![]() ��k��0����ͼ���һ�����㣮
��k��0����ͼ���һ�����㣮
��1��������������ʽ��
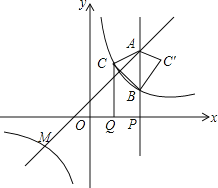
��2����P��x���������ϵ�һ�����㣬��OP��a��a��2��������P����ֱ��x���ֱ�ߣ��ֱ�һ�κ�����������������ͼ���ڵ�A��B����OP���е�Q��x��Ĵ��ߣ���������������ͼ���ڵ�C����ABC�����ABC����ֱ��AB�Գƣ�
�ٵ�a��4ʱ�����ABC��������
������AMC���AMC��������ȣ���a��ֵ ��
���𰸡���1��![]() ����2����3.5����a��ֵΪ3��
����2����3.5����a��ֵΪ3��
����������������1����һ�κ�������ʽ�ɵõ�M������Ϊ����3����2����Ȼ��ѵ�M��������뷴������������ʽ�����k��ֵ���ɵ÷�������������ʽ��
��2��������CC����AB�ڵ�D������ԳƵ���������֪AB��ֱƽ��OC�䣬��a=4ʱ�����ú�������ʽ�ɷֱ������A��B��C��D�����������ǿɵ�AB��CD�ij�����������á�ABC�������
������AMC���AMC��������ȣ��õ�C��C�䵽ֱ��MA�ľ�����ȣ��Ӷ��õ�C��A��C�����㹲�ߣ���![]() ������AP��PN���õ�
������AP��PN���õ�![]() ��a��1���ⷽ�̼��ɵõ����ۣ�
��a��1���ⷽ�̼��ɵõ����ۣ�
�������1����M����3��m������y��x��1����m����2��
������3����2������![]() ����k��6��������������ʽ�ǣ�
����k��6��������������ʽ�ǣ�![]() ��
��
��2��������CC�佻AB�ڵ�D����AB��ֱƽ��CC����
��a��4ʱ��A��4��5����B��4��1.5������AB��3.5��
�ߵ�QΪOP���е㣬��Q��2��0������C��2��3������D��4��3����
��CD��2����![]() ��3.5��2��3.5����
��3.5��2��3.5����![]() ��3.5��
��3.5��
�ڡ���AMC���AMC��������ȣ�
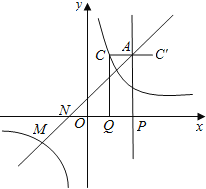
��C��C�䵽ֱ��MA�ľ�����ȣ���C��A��C�����㹲�ߣ���![]() ��
��
�֡�AP��PN����![]() ��a��1�����a��3��a����4����ȥ����
��a��1�����a��3��a����4����ȥ����
�൱��AMC���AMC���������ʱ��a��ֵΪ3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
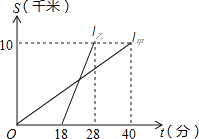
����Ŀ���ס�����������ͬ·��ǰ�����뵥λ10km����ѵ���IJμ�ѧϰ��ͼ��l����l���ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��S��km����ʱ��t���֣��仯�ĺ���ͼ������˵����
���ұȼ���ǰ12���ӵ�� �ڼ�ƽ���ٶ�Ϊ15ǧ��/Сʱ��
��������8km�������ף� ���ҳ���6���Ӻ��ϼף�
������ȷ����_____________����������ȷ����ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1��ƽ��ֱ������ϵxOy�У��ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵ�һ�����㣨��D���B��C���غϣ�������D��ֱ��y����![]() x��b������O��A��B�ڵ�E.
x��b������O��A��B�ڵ�E.
��1���ڵ�D�˶��Ĺ����У�����ODE�����ΪS����S��b�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2����ͼ2������E���߶�OA��ʱ������OABC����ֱ��DE�ԳƵ�ͼ��Ϊ����O��A��B��C�䣬C��B���ֱ�CB��OA�ڵ�D��M��O��A���ֱ�CB��OA�ڵ�N��E����֤���ı���DMEN�����Σ�
��3�����⣨2���е��ı���DMEN�У�ME�ij�Ϊ____________��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��������ǣ� ��
A. ��AP=BP,���P���߶ε��е� B. ����C���߶�AB�ϣ���AB=AC+BC
C. ��AC+BC>AB,���Cһ�����߶�AB�� D. ����֮�䣬�߶����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�C��D,ֱ��
���ڵ�C��D,ֱ��![]() ����һ��P.
����һ��P.
(1)��ͼ1����P��C��D֮���˶�ʱ����PAC����APB����PBD֮����ʲô��ϵ����˵�����ɡ�
(2)����P��C��D��������˶�ʱ(P����C��D���غϣ���ͼ2��3),��ֱ��д����PAC����APB����PBD֮����ʲô��ϵ������д���ɡ�

ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н����п��������ԣ���������������Ŀ��1000���ܡ�������Զ����ʵ����һ�����������������������Ŀ����������������Ŀ��ѡȡ������Ŀ��Ҫ��1000���ܱ�ѡ��������Զ����ʵ�����ѡһ��һ�����������������϶�ѡһ��
��1��д���������������������п���ѡ��Ľ����
��2���������б�������״ͼ�����������������������������ѡ��Ŀ��ȫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1����:![]() ��
��
(2)�ⲻ��ʽ��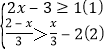
�����������,��ɱ���Ľ��:
�ⲻ��ʽ(1),��______________.
�ⲻ��ʽ(2),��_______________.
�Ѳ���ʽ(1)��(2)�Ľ⼯�������ϱ�ʾ����
![]()
��ԭ����ʽ��Ľ⼯Ϊ_________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������������Ľ�ˮ��ʶ���йز��ž͡�����Ϊ����Ч�Ľ�ˮ��ʩ������Բ�������������ʾ����飬�����ʾ���������ѡ���������ֻ��ѡ�����е�һ�A����̨��ط��ɷ��� B��������ˮ������ C���ƹ��ˮ���ĺͽ�ˮ���� D����ˮ��Խ�࣬ˮ��Խ�ߣ� E������
���ݵ�����������ͳ��ͼ����һ�������£�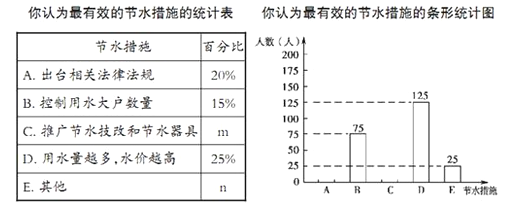
��1���˴γ������������Ϊ�ˣ�
��2���������ͳ��ͼ���ɵ�m=��n= ��
��3�������������Ϣֱ�Ӳ�ȫ����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C��D����P��ֱ��l3��һ����
��1����ͼ1������P���߶�CD���˶�ʱ����PAC����APB����PBD֮�����ʲô������ϵ�����������۲�˵�����ɣ�
��2������P��C��D���������˶�ʱ��P��![]() ���C��D���غϣ���ͼ2��ͼ3����������1���еĽ����Ƿ�����������������ֱ��д����PAC����APB����PBD֮���������ϵ������д���ɣ�
���C��D���غϣ���ͼ2��ͼ3����������1���еĽ����Ƿ�����������������ֱ��д����PAC����APB����PBD֮���������ϵ������д���ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com