
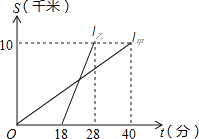
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
科目:初中数学 来源: 题型:
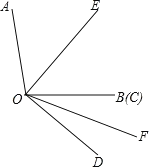
【题目】已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图1,当OB、OC重合时,求∠EOF的度数;
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<90)时,∠AOE﹣∠BOF的值是否为定值?若是定值,求出∠AOE﹣∠BOF的值;若不是,请说明理由.
(3)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<180)时,满足∠AOD+∠EOF=6∠COD,则n=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
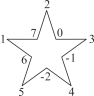
【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求![]() (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;
(2)交换其中任何两位数的位置后,![]() (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() , sinA=
, sinA=![]() , 求PC的长.
, 求PC的长.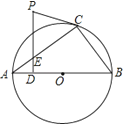
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC。

(1)若D为AC的中点,BD把三角形的周长分为24cm和30cm两部分,求△ABC三边的长;
(2)若D为AC上一点,试说明AC>![]() (BD+DC)。
(BD+DC)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
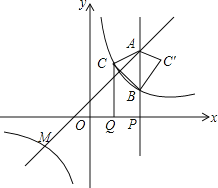
【题目】如图,点M(-3,m)是函数y=x+1与反比例函数![]() (k≠0)的图象的一个交点.
(k≠0)的图象的一个交点.
(1)求反比例函数表达式;
(2)点P是x轴正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.
①当a=4时,求△ABC′的面积;
②若△AMC与△AMC′的面积相等,求a的值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com