
����Ŀ����һ���ı��ε������Խ����ഹֱ����ȣ��������ı���Ϊ�������ı��Ρ�����ͼ1���ı���ABCD�У���AC=BD��AC��BD������ı���ABCDΪ�����ı��Σ����ݡ������ı��Ρ��Խ����ഹֱ�������ɵá������ı��Ρ���һ����Ҫ���ʣ��������ı��Ρ���������������Խ��߳˻���һ�룮����������Ϣ�ش� 
��1�������������ı��Ρ�����ǡ����ǡ�����
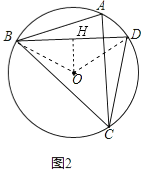
��2����ͼ2����֪��O���ڽ��ı���ABCD�ǡ������ı��Ρ�������O�İ뾶Ϊ6����BCD=60�㣮�������ı��Ρ�ABCD�������
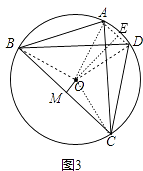
��3����ͼ3����֪��O���ڽ��ı���ABCD�ǡ������ı��Ρ���OM��BC��M����²�OM��AD��������ϵ����֤����Ľ��ۣ�
���𰸡�
��1������
��2���⣺����OB��OD����OH��BD��H����ͼ2����BH=DH��
�ߡ�BOD=2��BCD=2��60��=120�㣬
���OBD=30�㣬
��Rt��OBH�У��ߡ�OBH=30�㣬
��OH= ![]() OB=3��
OB=3��
��BH= ![]() OH=3
OH=3 ![]() ��
��
��BD=2BH=6 ![]() ��
��
��AC=BD=6 ![]() ��
��
�ࡰ�����ı��Ρ�ABCD�����= ![]() ��6
��6 ![]() ��6
��6 ![]() =54
=54
��3���⣺OM= ![]() AD���������£�
AD���������£�
����OB��OC��OA��OD����OE��AD��E����ͼ3��
��OE��AD��
��AE=DE��
�ߡ�BOC=2��BAC��
����BOC=2��BOM��
���BOM=��BAC��
ͬ���ɵá�AOE=��ABD��
��BD��AC��
���BAC+��ABD=90�㣬
���BOM+��AOE=90�㣬
�ߡ�BOM+��OBM=90�㣬
���OBM=��AOE��
�ڡ�BOM�͡�OAE��
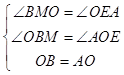 ��
��
���BOM�ա�OAE��
��OM=AE��
��OM= ![]() AD��
AD��
���������⣺��1�����εĶԽ�����ȵ�����ֱ�����Ծ��β��ǡ������ı��Ρ���
�ʴ�Ϊ���ǣ�
��1�����ݾ��ε����ʺ͡������ı��Ρ��Ķ�������жϣ���2������OB��OD����OH��BD��H����ͼ2�����ݴ��������õ�BH=DH������Բ�ܽǶ����õ���BOD=2��BCD=120�㣬�����õ��������ε����ʵá�OBD=30�㣬��Rt��OBH�пɼ����BH= ![]() OH=3
OH=3 ![]() ��BD=2BH=6
��BD=2BH=6 ![]() ����AC=BD=6
����AC=BD=6 ![]() ��Ȼ����������ı��Ρ���������������Խ��߳˻���һ����⣻��3������OB��OC��OA��OD����OE��AD��E����ͼ3�����ݴ��������õ�AE=DE��������Բ�ܽǶ����õ���BOM=��BAC����AOE=��ABD�������õȽǵ������ȵõ���OBM=��AOE�����֤����BOM�ա�OAE�õ�OM=AE��������OM=
��Ȼ����������ı��Ρ���������������Խ��߳˻���һ����⣻��3������OB��OC��OA��OD����OE��AD��E����ͼ3�����ݴ��������õ�AE=DE��������Բ�ܽǶ����õ���BOM=��BAC����AOE=��ABD�������õȽǵ������ȵõ���OBM=��AOE�����֤����BOM�ա�OAE�õ�OM=AE��������OM= ![]() AD��
AD��


 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������һ��ǽ��ǽ�ij��Ȳ�����45m������80m�������Χһ�����γ��أ� 
��1������Χ����ʹ���γ��ص����Ϊ750m2��
��2���ܷ�ʹ��Χ���γ��ص����Ϊ810m2 �� Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+3�ĶԳ�����ֱ��x=1��
��1����֤��2a+b=0��
��2��������x�ķ���ax2+bx��8=0��һ����Ϊ4���̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к���ͼ���У���x��0ʱ��y��x���������С���ǣ� ��
A.y=�� ![]()
B.y=x
C.y=x2
D.y=����x+1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������ͼ�����������⣺ 
��1�������������ʽ��
��2����xΪ��ֵʱ��y��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ���A��C������ֱ�ΪA��10��0����C��0��4������D��OA���е㣬��P��BC�����˶�������ODP������Ϊ5�ĵ���������ʱ����P������Ϊ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ��O�㣬E��F�ֱ���AB��BC���ϵ��е㣬����EF����EF= ![]() ��BD=4��������ABCD���ܳ�Ϊ�� ��
��BD=4��������ABCD���ܳ�Ϊ�� �� 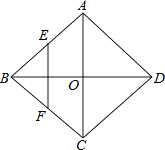
A.4
B.4 ![]()
C.4 ![]()
D.28
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��x2+mx+m��4������A��5����5�����������߶���ΪP��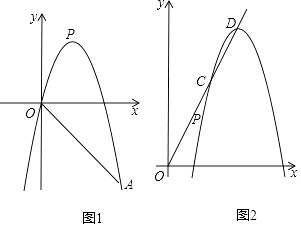
��1�����P�����ꣻ
��2����ֱ��OA�Ϸ�������������ȡһ��M������MO��MA�����MOA�����ȡ�����ʱ�ĵ�M���ꣻ
��3����ͼ1����ԭ������������OP�������ƽ�Ƶõ��µ������ߣ���������������OP����C��D���㣮�����߶�CD�ij����Ƿ�Ϊ��ֵ����������������ֵ����������˵�����ɣ�����ʾ������C��x1 �� y1����D��x2 �� y2������CD�ij���d= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�����Ϊ3cm2 �� EΪBC����һ�㣬��BAE=30�㣬FΪAE���е㣬����F��ֱ�߷ֱ���AB��DC�ཻ�ڵ�M��N����MN=AE����AM�ij����� cm��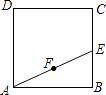
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com