练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线：y=x2+2(a－1)x+a2－2a(a>0)， P（2，3）在此抛物线上

    （1）求该抛物线的解析式

    （2）求直线 y=2x-2 与此抛物线的公共点个数；若有公共点，求出公共点的坐标．

    【答案】（1）；（2）公共点个数为1个；公共点的坐标为(1，0)．

    【解析】

    （1）将P点坐标代入抛物线的解析式中即可求出a的值；

    （2）将两个函数解析式联立成方程，解方程即可．

    （1）将P（2，3）代入y=x2+2（a-1）x+a2-2a得：

    得a2+2a-3=0，（a+3）（a-1）=0
    ∴a=-3或a=1

    ∵a>0

    ∴a=1

    ∴抛物线的解析式为：

    （2）根据题意得：

    整理得：

    解得：

    当x=1时，y=0

    故直线 y=2x-2 与此抛物线的公共点个数为1个；公共点的坐标为(1，0)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.

    (1)求证:四边形ADEF是平行四边形;

    (2)若∠ABC=60°,BD=6,求DE的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

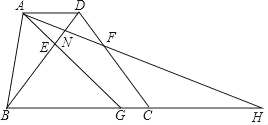
    【题目】如图，在梯形ABCD中，AD∥BC，BC＝18，DB＝DC＝15，点E、F分别在线段BD、CD上，DE＝DF＝5．AE的延长线交边BC于点G，AF交BD于点N、其延长线交BC的延长线于点H．

    （1）求证：BG＝CH；

    （2）设AD＝x，△ADN的面积为y，求y关于x的函数解析式，并写出它的定义域；

    （3）联结FG，当△HFG与△ADN相似时，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+bx+c与x轴交于点A（-1，0），B（3，0），与y轴交于点C（0，3），顶点为G．

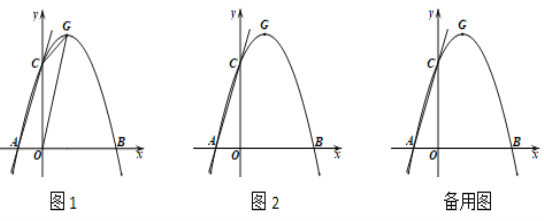
    （1）求抛物线和直线AC的解析式；

    （2）如图1，设E（m，0）为x正半轴上的一个动点，若△CGE和△CGO的面积满足S△CGE=S△CGO，求点E的坐标；

    （3）如图2，设点P从点A出发，以每秒1个单位长度的速度沿x轴向右运动，运动时间为ts，点M为射线AC上一动点，过点M作MN∥x轴交抛物线对称轴右侧部分于点N．试探究点P在运动过程中，是否存在以P，M，N为顶点的三角形为等腰直角三角形，若存在，求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数图象过A，B，C三点，点A的坐标为（﹣1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB＝OC．

    （1）求点C的坐标；

    （2）求二次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价2元收费；若每月用水量超过14吨,则超过部分每吨按市场价3.5元收费.小明家2月份用水20吨,交水费49元；3月份用水18吨,交水费42元．

    (1)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式；

    (2)小明家5月份用水30吨,则他家应交水费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

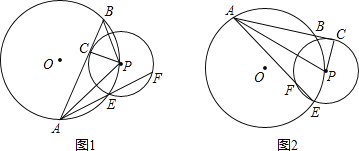
    【题目】如图，P是⊙O上的一个点，⊙P与⊙O的一个交点是E，⊙O的弦AB（或延长线）与⊙P相切，C是切点，AE（或延长线）交⊙P于点F，连接PA、PB，设⊙O的半径为R，⊙P的半径为r（R＞r），

    （1）如图1，求证：PAPB＝2rR；

    （2）如图2，当切点C在⊙O的外部时，（1）中的结论是否成立，试证明之；

    （3）探究（图2）已知PA＝10，PB＝4，R＝2r，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知x1、x2是一元二次方程2x2-2x+m+1=0的两个实根．

    （1）求实数m的取值范围；

    （2）如果m满足不等式7+4x1x2>x12+x22，且m为整数．求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，抛物线与轴交于A、B两点，与轴交于点C，直线经过A、C两点．

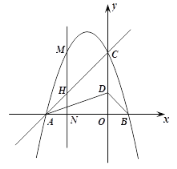
    （1）求抛物线的解析式；

    （2）点N是轴上的动点，过点N作轴的垂线，交抛物线与点M，交直线AC于点H．

    ①点D在线段OC上，连结AD、BD，当时，求的最小值；

    ②当时，将直线AD绕点A旋转，使直线AD与轴交于点P，请直接写出点P的坐标．

    查看答案和解析>>

    同步练习册答案