
【题目】如图所示,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,直线
轴交于点C,直线![]() 经过A、C两点.
经过A、C两点.
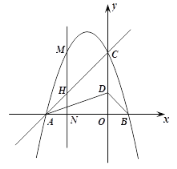
(1)求抛物线的解析式;
(2)点N是![]() 轴上的动点,过点N作
轴上的动点,过点N作![]() 轴的垂线,交抛物线与点M,交直线AC于点H.
轴的垂线,交抛物线与点M,交直线AC于点H.
①点D在线段OC上,连结AD、BD,当![]() 时,求
时,求![]() 的最小值;
的最小值;
②当![]() 时,将直线AD绕点A旋转
时,将直线AD绕点A旋转![]() ,使直线AD与
,使直线AD与![]() 轴交于点P,请直接写出点P的坐标.
轴交于点P,请直接写出点P的坐标.
【答案】(1)抛物线的解析式为![]() ;(2)①
;(2)①![]() 的最小值为4;②点P的坐标为
的最小值为4;②点P的坐标为![]() 或
或![]() .
.
【解析】
(1)先根据直线的解析式求出点A、C的坐标,再利用待定系数法求解即可得;
(2)①先根据抛物线的解析式求出点B的坐标,从而可得AB的长,再根据等量代换、两点之间线段最短即可得出答案;
②如图(见解析),分两种情况讨论:先根据点A、B坐标、等腰直角三角形的判定与性质得出DE、AE、OA的长,再根据相似三角形的判定与性质可得出OP的长,从而可得点P的坐标.
(1)对于![]() ,令
,令![]() 得
得![]() ,令
,令![]() 得
得![]() ,解得
,解得![]()
∴![]()
把点![]() 代入
代入![]() 得
得![]()
解得![]()
则抛物线的解析式为![]() ;
;
(2)①令![]()
解得![]()
∴![]()
![]()
∵![]()
∴![]()
由两点之间线段最短可知,![]() 的最小值为AB
的最小值为AB
即![]() 的最小值为4;
的最小值为4;
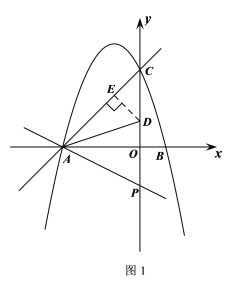
②由题意,分以下两种情况:
如图1,当直线AD绕点A顺时针旋转![]() 时,
时,![]()
∵![]()
∴![]()
![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
![]()
![]()
作![]() ,则
,则![]() 为等腰直角三角形
为等腰直角三角形
∵![]()
![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
在![]() 和
和![]() 中,
中,![]()
∴![]()
![]() ,即
,即![]()
解得![]()
![]()
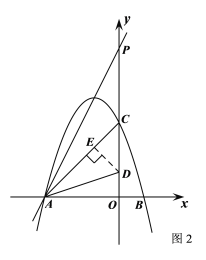
如图2,当直线AD绕点A逆时针旋转![]() 时,
时,![]()
∵![]()
∴![]()
作![]()
在![]() 和
和![]() 中,
中,![]()
∴![]()
![]() ,即
,即![]()
解得![]()
![]()
综上,点P的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线:y=x2+2(a-1)x+a2-2a(a>0), P(2,3)在此抛物线上
(1)求该抛物线的解析式
(2)求直线 y=2x-2 与此抛物线的公共点个数;若有公共点,求出公共点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
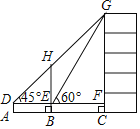
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(参考数据:![]() ≈14,
≈14,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
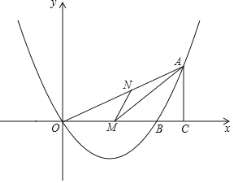
【题目】如图,已知二次函数 y=ax2+bx 的图象与 x 轴交于点 O(0,0)和 点 B,抛物线的对称轴是直线 x=3.点 A 是抛物线在第一象限上的一个动点, 过点 A 作 AC⊥x 轴,垂足为 C.S△AOB=3S△ABC,AC2=OCBC.
(1)求该二次函数的解析式;
(2)抛物线的对称轴与 x 轴交于点 M.连接 AM,点 N 是线段 OA 上的一点.当 ∠AMN=∠AOM 时,求点 N 的坐标;
(3)点 P 是抛物线上的一个动点.点 Q 是 y 轴上的一动点.当以 A,B,P,Q 四个点为顶点的四边形为平行四边形时,直接写出点 P 坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部数学专著,其中有这样一道名题:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几步及之?”意思是说:走路快的人走100步的时候,走路慢的才走了60步,走路慢的人先走100步,然后走路快的人去追赶,问走路快的人要走多少部才能追上?若设走路快的人要走x步才能追上走路慢的人,此时走路慢的人又走了y步,根据题意可列方程组为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
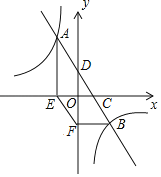
【题目】如图,已知一次函数y=﹣2x+b与反比例函数y=![]() 的图象有两个交点A(m,3)和B,且一次函数y=﹣2x+b与x轴、y轴分别交于点C、D.过点A作AE⊥x轴于点E;过点B作BF⊥y轴于点F,点F的坐标为(0,﹣2),连接EF,tan∠FEO=2.
的图象有两个交点A(m,3)和B,且一次函数y=﹣2x+b与x轴、y轴分别交于点C、D.过点A作AE⊥x轴于点E;过点B作BF⊥y轴于点F,点F的坐标为(0,﹣2),连接EF,tan∠FEO=2.
(1)求一次函数与反比例函数的解析式;
(2)求四边形AEFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画出抛物线y=﹣![]() (x﹣1)2+5的图象(要求列表,描点),回答下列问题:
(x﹣1)2+5的图象(要求列表,描点),回答下列问题:
(1)写出它的开口方向,对称轴和顶点坐标;
(2)当y随x的增大而增大时,写出x的取值范围;
(3)若抛物线与x轴的左交点(x1,0)满足n≤x1≤n+1,(n为整数),试写出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC中,OA=3,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
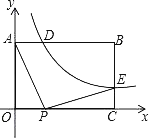
(1)求k的值和点E的坐标;
(2)点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A的坐标;
(2)当S△ABC=15时,求该抛物线的表达式;
(3)在(2)的条件下,经过点C的直线![]() 与抛物线的另一个交点为D.该抛物线在直线
与抛物线的另一个交点为D.该抛物线在直线![]() 上方的部分与线段CD组成一个新函数的图象。请结合图象回答:若新函数的最小值大于﹣8,求k的取值范围.
上方的部分与线段CD组成一个新函数的图象。请结合图象回答:若新函数的最小值大于﹣8,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com