
【题目】如图,已知∠1+∠2=180°,∠3=B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.

【答案】(1)证明见解析;(2)∠AED与∠C相等,理由见解析.
【解析】
(1)根据∠1+∠2=180°,∠1+∠DFE=180°,可得∠2=∠DFE,由内错角相等,两直线平行证明EF∥AB;
(2)根据∠3=∠ADE,∠3=∠B,由同位角相等,两直线平行证明DE∥BC,故可根据两直线平行,同位角相等,可得∠AED与∠C的大小关系.

解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点P是平行四边形ABCD对角线AC、BD的交点,若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4则S1、S2、S3、S4的关系为S1=S2=S3=S4.请你说明理由;
(2)变式1:如图2,点P是平行四边形ABCD内一点,连接PA、PB、PC、PD.若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,写出S1、S2、S3、S4的关系式;
(3)变式2:如图3,点P是四边形ABCD对角线AC、BD的交点若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,写出S1、S2、S3、S4的关系式.请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏,A型日光灯每盏进价为40元,售价为60元,B型日光灯每盏进价为50元,售价为80元.
(1)求10月份两种新型节能日光灯各购进多少盏?
(2)将10月份购买的日光灯从生产基地运往商场的过程中,A型日光灯出现![]() 的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润
的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润![]() 型日光灯在原售价基础上提高
型日光灯在原售价基础上提高![]() ,问A型日光灯调整后的售价为多少元?
,问A型日光灯调整后的售价为多少元?
(3)进入11月份,B型日光灯的需求量增大,于是商场在筹备“双十一”促销活动时,决定去甲、乙两个生产基地只购进一批B型日光灯,甲、乙生产基地给出了不同的优惠措施:
甲生产基地:B型日光灯出厂价为每盏50元,折扣如表一所示
乙生产基地:B型日光灯出厂价为每盏47元,同时当出厂总金额达一定数量后还可按表二返现金.
表一
甲生产基地 | |
一次性购买的数量 | 折扣数 |
不超过150盏的部分 |
|
超过150盏的部分 | 9折 |
表二
乙生产基地 | |
出厂总金额 | 返现金 |
不超过5640元 | 0元 |
超过5640元,但不超过9353元 | 返现300元 |
超过9353元 | 先返现出厂总金额的 |
已知该商场在甲生产基地购买B型日光灯共支付7350元,在乙生产基地购买B型日光灯共支付9006元,若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.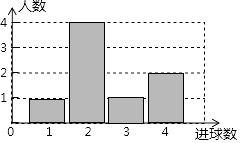
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为( )
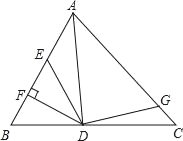
A. 12 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: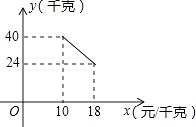
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com