
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: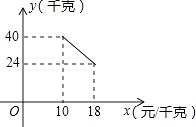
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
【答案】
(1)解:设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得:
![]() ,
,
解得 ![]() ,
,
∴y与x之间的函数关系式y=﹣2x+60(10≤x≤18);
(2)解:W=(x﹣10)(﹣2x+60)
=﹣2x2+80x﹣600
=﹣2(x﹣20)2+200,
对称轴x=20,在对称轴的左侧y随着x的增大而增大,
∵10≤x≤18,
∴当x=18时,W最大,最大为192.
即当销售价为18元时,每天的销售利润最大,最大利润是192元.
(3)解:由150=﹣2x2+80x﹣600,
解得x1=15,x2=25(不合题意,舍去)
答:该经销商想要每天获得150元的销售利润,销售价应定为15元.
【解析】(1)设y与x之间的函数关系式y=kx+b,把(10,40),(18,24)代入得到一个二元一次方程组,解之即可得出一次函数解析式.
(2)根据题意得W=(x﹣10)(﹣2x+60)=﹣2x2+80x﹣600(10≤x≤18),再由二次函数的性质得当x=18时,Wmax=192.
(3)又(2)得到的﹣2x2+80x﹣600=150(10≤x≤18),解之即可得出销售价格.
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°。
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C、∠B之间的数量关系(不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图和统计表.

(1)在图①中,“7分”所在扇形的圆心角等于 °;
(2)请你将图②所示的统计图补充完整;
(3)经计算,乙校的成绩的平均数是8.3分,中位数是8分,请写出甲校的成绩的平均数、中位数,并从平均数和中位数的角度分析哪个学校的成绩较好;
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列段文字,再解答问题:
已知在平面内有两点![]() 其两点间的距离公式为:
其两点间的距离公式为:
![]()
(1)已知点P(2,4)、Q(-3,-8),试求P、Q两点间的距离;
(2)已知点A(0,6)、B(-3,2)、C(3,2),判断线段AB、BC、AC中哪两条线段是相等的?并说明理由;
(3)已知点![]() 且MN=10,求
且MN=10,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )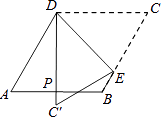
A.78°
B.75°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是:______;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )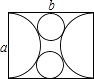
A.b= ![]() a
a
B.b= ![]() a
a
C.b= ![]()
D.b= ![]() a
a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com