练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．若式子（3-x）-1有意义，则x的取值范围是x≠3．

    分析 先将（3-x）-1转化为指数为正整数的形式，然后再讨论什么该式子什么时候有意义，本题得以解决．

    解答 解：∵$（3-x）^{-1}=\frac{1}{3-x}$，
    ∴3-x≠0，
    解得x≠3，
    即若式子（3-x）-1有意义，则x的取值范围是x≠3，
    故答案为：x≠3．

    点评 本题考查负整数指数幂，解题的关键是运用转化的数学思想，将原式转化为正整数幂的形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

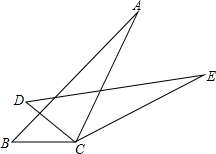    3．如图所示，∠B=∠D，BC=DC，要判定△ABC≌△EDC，当添加条件∠ACB=∠ECD时，可根据”ASA“判定；当添加条件∠A=∠E时．可根据“AAS”判定；当添加条件AB=ED时，可根据“SAS”判定．

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省南雄市九年级下学期模拟考试数学试卷（解析版） 题型：填空题

    如图，已知矩形ABCD中，AB＝8，BC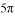＝．分别以B、D为圆心，AB为半径画弧，两弧分别交对角线BD于点E、F，则图中阴影部分的面积为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．（1）如图1，将∠EAF绕着正方形ABCD的顶点A顺时针旋转，∠EAF的两边交BC于E，交CD于F，连接EF．若∠EAF=45°，BE、DF的长度是方程x2-5x+6=0的两根，请直接写出EF的长；
    （2）如图2，将∠EAF绕着四边形ABCD的顶点A顺时针旋转，∠EAF的两边交CB的延长线于E，交DC的延长线于F，连接EF．若AB=AD，∠ABC与∠ADC互补，∠EAF=$\frac{1}{2}$∠BAD，请直接写出EF与DF、BE之间的数量关系，并证明你的结论；
    （3）在（2）的前提下，若BC=4，DC=7，CF=2，求△CEF的周长．
    ①EF的长为：5；
    ②数量关系：EF=DF-BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

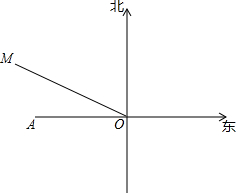    8．如图，根据天气预报，台风中心位于A市正东方向300km的点O处，正以20km/h的速度向北偏西60°方向移动，距离台风中心250km范围内都会受到影响，若台风移动的速度和方向不变，则A市受台风影响的时间是有多长？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

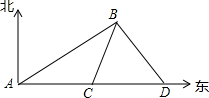    17．如图，某船在海上航行，在A处观测到灯塔B在北偏东60°方向上，该船以每小时15海里的速度向东航行到达C处，观测到灯塔B在北偏东30°方向上，继续向东航行到D处，观测到灯塔B在北偏西30°方向上，当该船到达D处时恰与灯塔B相距60海里．
    （1）判断△BCD的形状；
    （2）求该船从A处航行至D处所用的时间；
    （3）若该船从A处向东航行6小时到达E处，观测灯塔B，灯塔B在什么方向上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

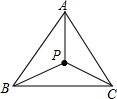    4．如图，点P是正△ABC内一点．
    （1）以点B为旋转中心，将△PBC逆时针旋转60°，试画出旋转后的图形；
    （2）若PB=3，PC=4，∠BPC=150°，请求出PA的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

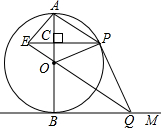    1．如图，AB是⊙0的直径，BM切⊙0于点B，点P是⊙0上的一个动点（不经过A、B两点），过点0作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ．
    （1）求证：PQ与⊙0相切；
    （2）若直径AB的长为12，PC=2EC，$\frac{OC}{AC}$=$\frac{EC}{PC}$，求PC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

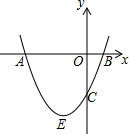    2．如图，抛物线y=x2+bx+c与y轴交于点C，与x轴交于点A，B，点A在点B的左侧，点A的坐标为A（-3，0），且AB=4．
    （1）求抛物线的解析式；
    （2）若过点C且与x轴平行的直线交抛物线于另一个点D，抛物线的顶点为点E，试判断△CDE的形状，并求其面积．

    查看答案和解析>>

    同步练习册答案