
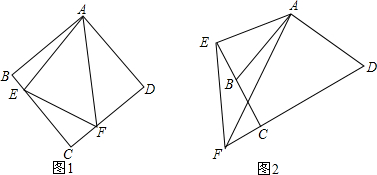
分析 (1)先证明△ABE≌△ADM,再证明△AEF≌△AMF,得到EF=DF+BE即可;
(2)先证明△ADM≌△ABE,再证明△EAF≌△MAF,即可;
(3)直接计算△CEF的周长=EF+BE+BC+CF=DF+BC+CF=9+4+2=15.
解答 (1)解:如图1,
延长CD使DM=BE,连接AM;
在△ABE和△ADM中,$\left\{\begin{array}{l}{AB=AD}\\{∠ABE=∠ADM=90°}\\{BE=DM}\end{array}\right.$
∴△ABE≌△ADM,
∴AE=AM,∠EAB=∠DAM,
∵∠EAF=45°,且∠EAB=∠DAM,
∴∠BAF+∠DAM=45°,即∠MAF=45°=∠EAF,
又∵AE=AM,AF=AF,
∴△AEF≌△AMF,
∴EF=FM,
∵FM=DF+DM,
∴EF=DF+NB,
即EF=DF+BE;
∵BE、DF的长度是方程x2-5x+6=0的两根,
∴BE=2,DF=3,
∴EF=DF+BE=3+2=5,
(2)证明:
如图2,在DF上截取DM=BE,
∵∠D+∠ABC=∠ABE+∠ABC=180°,
∴∠D=∠ABE,
∴AD=AB,
∴△ADM≌△ABE,
∴AM=AE,
∴∠DAM=∠BAE;
∵∠EAF=∠BAE+∠BAF=∠DAM+∠BAF=∠BAD-∠FAM=$\frac{1}{2}$∠BAD,
∴∠MAF=$\frac{1}{2}$∠BAD,
∴∠EAF=∠MAF;
∵AF是△EAF与△MAF的公共边,
∴△EAF≌△MAF,
∴EF=MF;
∵MF=DF-DM=DF-BE,
∴EF=DF-BE.
(3)由上面的结论知:DF=EF+BE;
∵BC=4,DC=7,CF=2,
∴DF=CD+CF=9
∴△CEF的周长=EF+BE+BC+CF=DF+BC+CF=9+4+2=15.
即△CEF的周长为15.
①EF=DF-BE=FC+CD-BE=5
②和(2)方法一样,EF=DF-BE.
故答案为EF=DF-BE.
点评 此题是几何变换的综合题,主要考查的是全等三角形的性质和判定,通过两步全等来证得到关键的两组线段相等是本题的基本思路.


科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图形在第一象限相交于点A(1,-k+4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
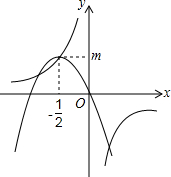 如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.
如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:单选题
一个正多边形的内角是135°,这个多边形的边数是( )
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com