
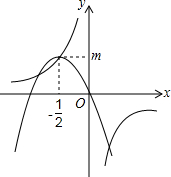
 如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.
如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$. 分析 由点在二次函数与反比例函数图象上,再结合二次函数的对称轴为-$\frac{b}{2a}=-\frac{1}{2}$,可得出关于a、b、m的三元一次方程组,解方程组即可得出m的值,再根据m>0,即可得出结论.
解答 解:根据已知得:$\left\{\begin{array}{l}{m=-\frac{2}{a}}\\{m=\frac{1}{4}a-\frac{1}{2}b}\\{-\frac{b}{2a}=-\frac{1}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=b=2\sqrt{2}}\\{m=-\frac{\sqrt{2}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{a=b=-2\sqrt{2}}\\{m=\frac{\sqrt{2}}{2}}\end{array}\right.$.
∵m>0,
∴m=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次函数的性质以及解三元一次方程组,解题的关键是根据已知列出关于a、b、m的三元一次方程组.本题属于基础题,难度不大,解决该题型题目时,根据点在函数图象上以及二次函数的性质列出方程(或方程组)是关键.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
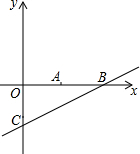 在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).
在平面直角坐标系xOy中,点A、点B、点C坐标分别为(5,0)、(10,0)、(0,-5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
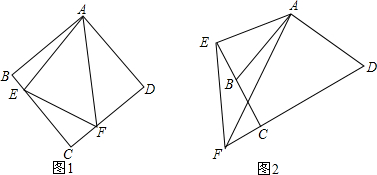
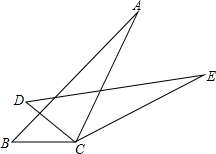 如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.
如图所示,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件∠ACB=∠ECD时,可根据”ASA“判定;当添加条件∠A=∠E时.可根据“AAS”判定;当添加条件AB=ED时,可根据“SAS”判定.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:判断题
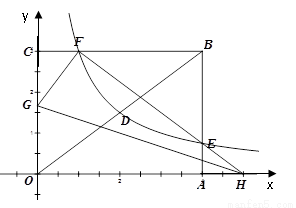
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数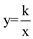 (k≠0)在第一象限内的图象经过点D、E,且
(k≠0)在第一象限内的图象经过点D、E,且
cos∠BOA=
(1)求边AB的长;
(2)求反比例函数的解析式和m的值;
(3)若反比例函数的图象与矩形的边BC交于点F,点G、H分别是Y轴、X轴上的点,当
△OGH≌△FGH时,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:填空题
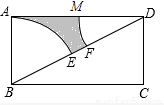
如图,已知矩形ABCD中,AB=8,BC=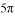 .分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为__________.
.分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
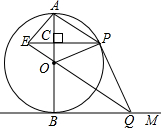 如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.
如图,AB是⊙0的直径,BM切⊙0于点B,点P是⊙0上的一个动点(不经过A、B两点),过点0作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com