
 如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )
如图,CD为△ABC的中线,且CD⊥AC,O为BC边上一点,以O为圆心,0C为长半径作⊙O,若⊙O与AB恰好相切于点D,则tanB=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
分析 连接OD、DE,如图,设⊙O的半径为r,先证明DE∥AC,再利用点D为AB的中点得到点E为BC的中点,接着利用切线的性质得OD⊥AB,然后在Rt△BOD中利用勾股定理计算出BD后根据正切的定义求解.
解答 解:连接OD、DE,如图,设⊙O的半径为r,
∵CE为直径,
∴∠CDE=90°,
∵CD⊥AC,
∴∠ACD=90°,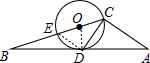
∵DE∥AC,
∵点D为AB的中点,
∴DE为△ABC的中位线,
∴点E为BC的中点,
∴BE=CE=2r,
∵AB为切线,
∴OD⊥AB,
在Rt△BOD中,OD=r,OB=BE+OE=3r,
∴BD=$\sqrt{(3r)^{2}-{r}^{2}}$=2$\sqrt{2}$r,
∴tanB=$\frac{OD}{BD}$=$\frac{r}{2\sqrt{2}r}$=$\frac{\sqrt{2}}{4}$.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决本题的关键是证明点E为BC的中点.


科目:初中数学 来源: 题型:选择题
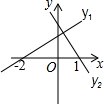 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )| A. | x<-2 | B. | -2<x<1 | C. | x>0 | D. | x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
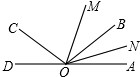 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.
如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )
如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
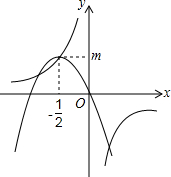 如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.
如图,反比例函数y=$\frac{1}{ax}$(a≠0)的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则m=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:判断题
春季是流感的高发期,有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?如果按照这样的传染速度,三轮传染后有多少人患流感?
查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:单选题
一个正多边形的内角是135°,这个多边形的边数是( )
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com