
【题目】已知二次函数y=ax2﹣2ax+k(a、k为常数,a≠0),线段AB的两个端点坐标分别为A(﹣1,2),B(2,2).
(1)该二次函数的图象的对称轴是直线 ;
(2)当a=﹣1时,若点B(2,2)恰好在此函数图象上,求此二次函数的关系式;
(3)当a=﹣1时,当此二次函数的图象与线段AB只有一个公共点时,求k的取值范围;
(4)若k=a+3,过点A作x轴的垂线交x轴于点P,过点B作x轴的垂线交x轴于点Q,当﹣1<x<2,此二次函数图象与四边形APQB的边交点个数是大于0的偶数时,直接写出k的取值范围.
【答案】(1)x=1;(2)y=﹣x2+2x+2;(3)2<k≤5或k=1;(4)2≤k<![]() 或k<0
或k<0
【解析】
(1)根据二次函数y=ax2﹣2ax+k(a、k为常数,a≠0)即可求此二次函数的对称轴;
(2)当a=﹣1时,把B(2,2)代入即可求此二次函数的关系式;
(3)当a=﹣1时,根据二次函数的图象与线段AB只有一个公共点,分三种情况说明:当抛物线顶点落在AB上时,k+1=2,k=1;当抛物线经过点B时,k=2;当抛物线经过点A时,k=5,即可求此k的取值范围;
(4)当k=a+3,根据题意画出图形,观察图形即可求此k的取值范围.
解:(1)二次函数y=ax2﹣2ax+k(a、k为常数,a≠0),
二次函数的图象的对称轴是直线x=1.
故答案为x=1;
(2)当a=﹣1时,y=﹣x2+2x+k
把B(2,2)代入,得 k=2,
∴y=﹣x2+2x+2
(3)当a=﹣1时,
y=﹣x2+2x+k
=﹣(x﹣1)2+k+1
∵此二次函数的图象与线段AB只有一个公共点,
当抛物线顶点落在AB上时,k+1=2,k=1
当抛物线经过点B时,k=2
当抛物线经过点A时,
﹣1﹣2+k=2,k=5
综上所述:2<k≤5或k=1;
(4)当k=a+3时,
y=ax2﹣2ax+a+3
=a(x﹣1)2+3
所以顶点坐标为(1,3)
∴a+3<3
∴a<0.
如图,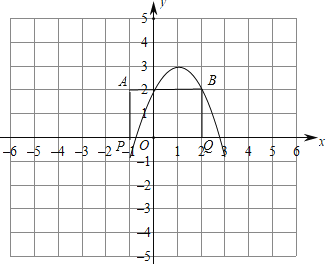
过点A作x轴的垂线交x轴于点P,过点B作x轴的垂线交x轴于点Q,
∴P(﹣1,0),Q(2,0)
当﹣1<x<2,此二次函数图象与四边形APQB的边交点个数是大于0的偶数,
当抛物线过点P时,
a+2a+a+3=0,解得a=﹣![]()
∴k=a+3=![]() ,
,
当抛物线经过点B时,
4a﹣4a+a+3=2,解得a=﹣1,
∴k=2,
当抛物线经过点Q时,
4a﹣4a+a+3=0,解得a=﹣3,
∴k=0
综上所述:2≤k<![]() 或k<0.
或k<0.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
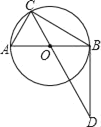
【题目】如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD.已知BC=BD,AB=4.
(1)若BC=2![]() ,求证:BD是⊙O的切线;
,求证:BD是⊙O的切线;
(2)BC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣![]() ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程![]() 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直角坐标系中画出二次函数![]() 与二次函数
与二次函数![]() 的图形.
的图形.
(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;
(2)说出两个函数图象的性质的相同点与不同点.
查看答案和解析>>
科目:初中数学 来源: 题型:
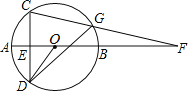
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G为弧BC上一动点,CG与AB的延长线交于点F,连接OD.
(1)判定∠AOD与∠CGD的大小关系为 ,并求证:GB平分∠DGF.
(2)在G点运动过程中,当GD=GF时,DE=4,BF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,交x轴于A,B两点
,交x轴于A,B两点![]() 点A在点B的左侧
点A在点B的左侧![]() .
.

![]() 求抛物线的解析式,并写出顶点M的坐标;
求抛物线的解析式,并写出顶点M的坐标;
![]() 连接OC,CM,求
连接OC,CM,求![]() 的值;
的值;
![]() 若点P在抛物线的对称轴上,连接BP,CP,BM,当
若点P在抛物线的对称轴上,连接BP,CP,BM,当![]() 时,求点P的坐标.
时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为“节能减排,保护环境”,某村计划建造A、B两种型号的沼气池共20个,以解决所有农户的燃料问题.据市场调查:建造A、B两种型号的沼气池各1个,共需费用5万元;建造A型号的沼气池3个,B种型号的沼气池4个,共需费用18万元.
(1)求建造A、B两种型号的沼气池造价分别是多少?
(2)设建造A型沼气池x个,总费用为y万元,求y与x之间的函数关系式;若要使投入总费用不超过52万元,至少要建造A型沼气池多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com