
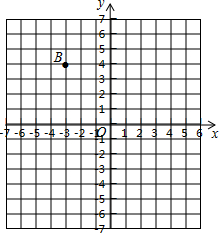
 如图,在直角坐标平面内,已知点A的坐标(-2,0),
如图,在直角坐标平面内,已知点A的坐标(-2,0),分析 (1)根据图示直接写出答案;
(2)关于原点对称的点的横纵坐标与原来的互为相反数;关于y轴对称的点的坐标,纵坐标不变,横坐标互为相反数;
(3)根据四边形ABDC的面积=S△ABD+S△ADC即可解答;
(4)求出△ADE的高为4,即可解答;
(5)根据三角形的面积公式求得OF的长度即可.
解答 解:(1)根据图示知,点B的坐标为(-3,4);
(2)由(1)知,B(-3,4),
∴点B关于原点对称的点C的坐标是(3,-4);
∵点A的坐标(-2,0),
∴点A关于y轴对称的点D的坐标是(2,0);
(3)如图,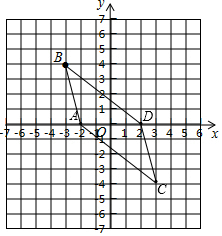
四边形ABDC的面积=S△ABD+S△ADC=4×4×$\frac{1}{2}$+4×4×$\frac{1}{2}$=16.
(4)S△ABC=S△ABO+S△ACO=$2×4×\frac{1}{2}+2×4×\frac{1}{2}$=8,
∵S△ADE=S△ABC,
∴4•h•$\frac{1}{2}$=8,
∴h=4,
∵AD在x轴上,
∴直角坐标平面上找一点E,只要点E的纵坐标的绝对值为4即可,
∴直角坐标平面内点E有无数个.
(5)∵S△ADF=S△ABC,AD=4,S△ABC=8
∴OF=4
∴那么点F的所有可能位置是(0,4)或(0,-4).
故答案为:(1)(-3,4);(2)(3,-4),(2,0);(3)16;(4)无数;(5)(0,4)或(0,-4).
点评 本题综合考查了三角形的面积、坐标与图形性质、关于坐标轴对称的点的坐标以及坐标图形变换与旋转.解答此类题目时,要将图形画出来,利用“数形结合”的数学思想解题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 近似数1.8与1.80表示的意义不一样 | |
| B. | 5.0万精确到万位 | |
| C. | 0.20精确到0.01 | |
| D. | 0.345×105用科学记数法表示为3.45×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2x2-x+3 | B. | y=-2x2+4 | C. | y=-2x2+4x+8 | D. | y=-2x2+4x+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com