
【题目】某校为学生装一台直饮水器,课间学生到直饮水器打水.他们先同时打开全部的水笼头放水,后来又关闭了部分水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,直饮水器的余水量![]() (升)与接水时间
(升)与接水时间![]() (分)的函数图象如图,请结合图象回答下列问题:
(分)的函数图象如图,请结合图象回答下列问题:
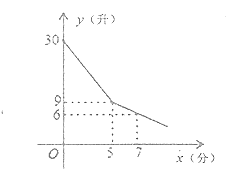
(1)求当![]() 时,
时,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)假定每人水杯接水0.7升,要使40名学生接水完毕,课间10分钟是否够用?请计算回答.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】学习有理数得乘法后,老师给同学们这样一道题目:
计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
聪聪:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
明明:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:29![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )
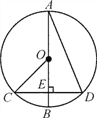
A. ∠BOC=2∠BAD B. CE=EO C. ∠OCE=40° D. AD=2OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.如果一个图形是中心对称图形,那么它一定不是轴对称图形
B.正方形是轴对称图形,它共有两条对称轴
C.等边三角形是旋转对称图形,它的最小旋转角等于![]() 度
度
D.平行四边形是中心对称图形,其对称中心是它的一条对角线的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知三角形纸片![]() ,将纸片折叠,使点
,将纸片折叠,使点![]() 与点
与点![]() 重合,折痕分别与边
重合,折痕分别与边![]() 交于点
交于点![]() .
.
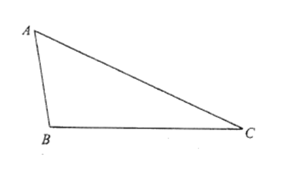
(1)画出直线![]() ;
;
(2)若点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,请画出点
,请画出点![]() ;
;
(3)在(2)的条件下,联结![]() ,如果
,如果![]() 的面积为2,
的面积为2,![]() 的面积为
的面积为![]() ,那么
,那么![]() 的面积等于 .
的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.
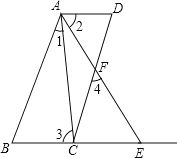
解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.
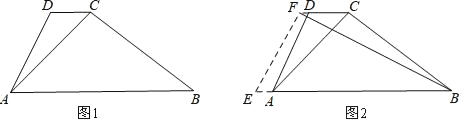
(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底间时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
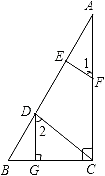
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月3日至2019年2月20日,“第一届”成都金沙太阳节在金沙遗址博物馆成功举办,用世界文明展览,主题灯展,园林花艺,美食演绎等一系列文化活动,与玛雅这一著名的中美洲文明结下不解之缘,为成都人打造了一个博物馆里的“文化年”.春节当天,小杰于下午![]() 点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离
点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离![]() (千米)与他离家的时间
(千米)与他离家的时间![]() (小时)之间的图像.根据图像,完成下面的问题:
(小时)之间的图像.根据图像,完成下面的问题:
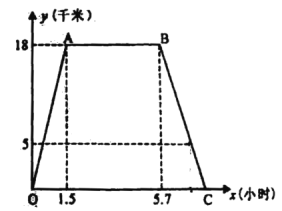
(1)小杰家距金沙遗址博物馆 千米,他乘车去金沙遗址博物馆的速度是 千米/小时;
(2)已知晚上![]() 点时,小杰距家
点时,小杰距家![]() 千米,请通过计算说明他何时才能回到家?
千米,请通过计算说明他何时才能回到家?
(3)请直接写出小杰回家过程中![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com