
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )
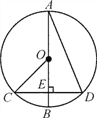
A. ∠BOC=2∠BAD B. CE=EO C. ∠OCE=40° D. AD=2OB
【答案】A
【解析】
根据“垂径定理”和“圆的有关性质”进行分析即可即可.
如下图,连接OD,
∵在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,
∴∠OEC=90°,![]() ,
,
∴∠BOC=∠BOD,
∵∠BOD=2∠BAD=40°,
∴∠BOC=2∠BAD=40°,即A中结论正确;
∴∠OCE=180°-90°-40°=50°,即C中结论不成立;
∴∠COE![]() ∠OCE,
∠OCE,
∴CE![]() EO,即B中结论不成立;
EO,即B中结论不成立;
∵AB是⊙O的直径,而AD是⊙O的一条非直径的弦,
∴AB>AD,
∵AB=2OB,
∴AD<2OB,即D中结论不成立.
综上所述,上述四个选项中,只有A中的结论成立.
故选A.

点睛;熟悉“垂径定理和圆的相关性质”是解答本题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】定义一次函数y=px+q的特征数为[p,q].如:y=3x-1的特征数是[3,-1]
(1)若某正比例函数的特征数是[k+2, ![]() ],求k的值.
],求k的值.
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且△OAB的面积为4(O为原点),求过A、B两点的一次函数的特征数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简与求值
(1)求3x2+x+3(x2﹣![]() x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.
(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣![]() )2=0
)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
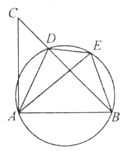
(1)求证:AE=AB;
(2)若∠CAB=90°,cos∠ADB=![]() ,BE=2,求BC的长.
,BE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
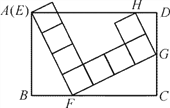
【题目】如图,由8个大小相等的小正方形构成的图案,它的四个顶点 E,F,G,H分别在矩形ABCD的边AB,BC,CD,DA上,若AB=4,BC=6,则DG的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
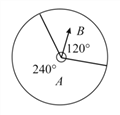
【题目】有一个转盘如图,让转盘自由转动,指针落在分界线重新转动.
(1)让转盘自由转动一次,求落在A区域和落在B区域的概率;
(2)让转盘自由转动两次,求两次都落在A区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为学生装一台直饮水器,课间学生到直饮水器打水.他们先同时打开全部的水笼头放水,后来又关闭了部分水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,直饮水器的余水量![]() (升)与接水时间
(升)与接水时间![]() (分)的函数图象如图,请结合图象回答下列问题:
(分)的函数图象如图,请结合图象回答下列问题:
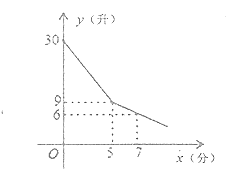
(1)求当![]() 时,
时,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)假定每人水杯接水0.7升,要使40名学生接水完毕,课间10分钟是否够用?请计算回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
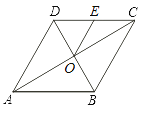
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com