
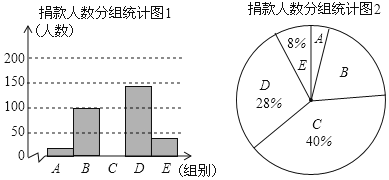
����Ŀ����У���㰮�����ų���ȫУѧ���μ�����ע�����ͯ����Ը��������Դ˴λ���г������飬�õ�һ��ѧ�������������ݣ���������������ͼ��ʾ��ͳ��ͼ��ͼ����Ϣ������������֪A��B�����������ı�Ϊ1��5������������Ϣ����������⣮
��� | ����x/Ԫ | ���� |
A | 1��x��10 | |
B | 10��x��20 | 100 |
C | 20��x��30 | |
D | 30��x��40 | |
E | x��40 |
��1��a= ����������������������� ��
��2����ȫ�������������ͳ��ͼ1����
��3������A�����ƽ����Ϊ5Ԫ��B�����ƽ����Ϊ15Ԫ��C�����ƽ����Ϊ25Ԫ��D�����ƽ����Ϊ35Ԫ��E�����ƽ����Ϊ50Ԫ��ȫУ����2000��ѧ���μӴ˴λ��������ƴ˴λ���Գ���ƿ�Ľ���ԼΪ����Ԫ��
���𰸡���1��20��500����2����ȫ�������������ͳ��ͼ����ͼ��ʾ������������3�����ƴ˴λ���Գ���ƿ�Ľ���ԼΪ54000Ԫ��
��������
��1����B������Ϊ100��A��B�����������ı�Ϊ1��5�ɵ�a��ֵ����A��B�������ͳ�������ռ�ٷֱȿɵ���������
��2�������C���������̶��ɲ�ȫͼ�Σ�
��3�����������500��ѧ����ƽ����������ٳ����������ɵã�
��1��a=100��![]() =20��
=20��
���ε��������������ǣ���100+20������1-40%-28%-8%��=500��
�ʴ�Ϊ��20��500��
��2����500��40%=200��
��C�������Ϊ200��
��ȫ�������������ͳ��ͼ1������ͼ��ʾ��
��3����A���Ӧ�ٷֱ�Ϊ![]() ��100%=4%��B���Ӧ�İٷֱ�Ϊ
��100%=4%��B���Ӧ�İٷֱ�Ϊ![]() ��100%=20%��
��100%=20%��
�����500��ѧ����ƽ�������Ϊ5��4%+15��20%+25��40%+35��28%+50��8%=27��Ԫ����
����ƴ˴λ���Գ���ƿ�Ľ���ԼΪ2000��27=54000��Ԫ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2k+3��x+k2��0����������ȵ�ʵ����x1��x2����![]() ����1����k��ֵΪ_____��
����1����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԥ���������ڶ�Ա��ʦѧϰ������ʮ�Ŵ��������У���֯ȫ����ʦ�μ���������ʮ�Ŵ�֪ʶ�����������������ȡ��ijУ���ֽ�ʦ�ijɼ������ӵͷֵ��߷ֽ��ɼ��ֳ�A��B��C��D��E���飺x��60��60��x��70��70��x��80��80��x��90��90��x��100������100�֣������Ƴ�����������������ͳ��ͼ��

���������ṩ����Ϣ����������⣺
��1��D������Ӧ��Բ�Ľ����� �ȣ������гɼ�����λ�������� ���У�
��2����ȫ����ͳ��ͼ��
��3������D��E����ɼ���Ϊ���㣬ȫ���μӱ���������ʮ�Ŵ�֪ʶ����������2000����ʦ������ȫ���μӾ����ﵽ����Ľ�ʦ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��x1��y1����B��x2��y2����C��x3��y3���ڷ���������y= ![]() ��ͼ���ϣ���x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ�ǣ�������
��ͼ���ϣ���x1��x2��0��x3����y1��y2��y3�Ĵ�С��ϵ�ǣ�������
A. y1��y2��y3B. y2��y3��y1C. y3��y2��y1D. y2��y1��y3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��AOB�ǵȱ������Σ���A�������ǣ�0��4������B��һ���ޣ���P��t��0����x���ϵ�һ�����㣬����AP��������AOP���ŵ�A����ʱ�뷽����ת��ʹ��AO��AB�غϣ�����OD��PD������OPD��
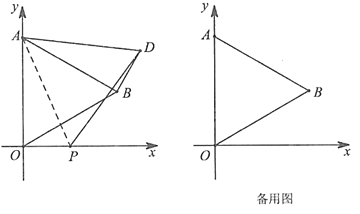
��1����t��![]() ʱ����DP�ij�
ʱ����DP�ij�
��2���ڵ�P�˶������У������������γɵ���OPD���ΪS
�ٵ�t��0ʱ����S��t֮��ĺ�����ϵʽ
�ڵ�t��0ʱ��Ҫʹs��![]() ����ֱ��д�����з��������ĵ�P������.
����ֱ��д�����з��������ĵ�P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������L��y=ax2+bx+3��x�ύ��A��1��0����B��3��0�����㣬��y�ύ�ڵ�C������ΪD��
��1���������ߵĺ�������ʽ������D�����ꣻ
��2������������L��y��ƽ�ƺ�õ�������L����������L��������E��4��1������y��Ľ���ΪC��������ΪD������������L�����Ƿ���ڵ�M��ʹ����MCC�����������MDD�������2���������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ��������Խ��߽�������ı��ε����ɷ�����������ı��ν��������ı���������һ���ı����������ɷ��ߣ����Ϊ�������ı��Σ�
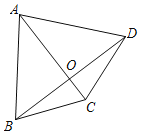
��1�������ı���һ���������ı��ε����� ��������ţ�
��ƽ���ı��Σ��ھ��Σ������Σ��������Σ�
������Ӧ�ã�
��2����ͼ���ھ����ı���ABCD�У�AC��AD����AC��ֱƽ��BD������BAD��80�������BCD�Ķ�����
���������
��3���������ı���ABCD�У�AB��AD��CD����A��90����AC���ı���ABCD���ɷ��ߣ���ֱ��д����BCD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ٵ��ˣ�����ӭ���ֻ��г�������������ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ�Ͷ��15.5��Ԫ�ʽ�ȫ�����ڹ��������ֻ����ɲ�������ȫ�����ۺ�ɻ�ë������2��Ԫ����ë����=���ۼ۩����ۣ�����������
��1�����̳�Ҫ�뾡���ܶ�Ĺ��������ֻ���Ӧ�ð��������Ľ��������������������ֻ���
��2��ͨ���г����У����̳������ڼ����ֻ��������ķ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1���ھ��� ABCD �У��� E �� lcm/s ���ٶȴӵ� A ��� D �˶����˶�ʱ��Ϊ t��s�������� BE������ E �� EF��BE���� CD �� F���� EF Ϊֱ������O��
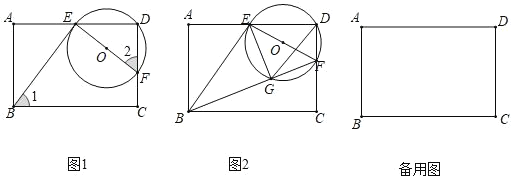
��1����֤����1����2��
��2����ͼ 2������ BF������O �ڵ� G�������� EG����֪ AB��4��AD��6��
���ú� t �Ĵ���ʽ��ʾ DF �ij�
������ DG������EGD ���� EG Ϊ���ĵ��������Σ��� t ��ֵ��
��3������ OC���� tan��BFC��3 ʱ��ǡ�� OC��EG����ֱ��д�� tan��ABE ��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com