
【题目】已知:如图∠1=∠2,∠3=∠4,∠5=∠6,∠1=60°,∠7=20°
(1)试说明AC⊥BD
(2)求∠3及∠5的度数
(3)求四边形ABCD各内角的度数.

【答案】(1)见解析;(2)30°,70°;(3)∠DAB =60°,∠ABC =80°,∠DCB =140°,∠ADC =80°
【解析】
(1)根据三角形内角和定理即可证得∠1+∠3=90°,则在△AOD中,利用内角和定理即可求得∠AOD=90°,即可证得;
(2)根据直角三角形的两个锐角互余即可求解;
(3)根据根据(2)即可求得∠DAB,∠ADC,∠DCB的度数,然后根据四边形的内角和定理即可求得∠ABC的度数.
(1)∵∠1+∠2+∠DAB=180°,
即∠1+∠2+∠3+∠4=180°,
又∵∠1=∠2,∠3=∠4,
∴∠1+∠3=90°,
∵∠1+∠3+∠AOD=90°,
∴∠AOD=90°,
∴AC⊥BD;
(2)∵∠1+∠3=90°,
∴∠3=90°∠1=90°60°=30°.
∵AC⊥BD,
∴∠COD=90°,
∴∠5+∠7=90°,
∴∠5=90°∠7=70°;
(3)∠DAB=2∠3=60°,
∠ADC=∠1+∠7=60°+20°=80°,
∠DCB=∠5+∠6=70°+70°=140°,
则∠ABC=360°∠DAB∠ADC∠DCB=80°.


科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.平面直角坐标系![]() 为原点,长方形
为原点,长方形![]() 的顶点
的顶点![]() 在坐标轴上,点
在坐标轴上,点![]() ,
,![]() ,且己知
,且己知![]() 是64的立方根,
是64的立方根,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)如图1,有两动点![]() 点从
点从![]() 点出发沿
点出发沿![]() 轴负方向以1个单位长度每秒的速度匀速移动,
轴负方向以1个单位长度每秒的速度匀速移动,![]() 点从
点从![]() 点出发以2个单位长度每秒的速度沿
点出发以2个单位长度每秒的速度沿![]() 的路线匀速移动,
的路线匀速移动,![]() 点到达
点到达![]() 点整个运动随之结束.若长方形对角线
点整个运动随之结束.若长方形对角线![]() 的交点
的交点![]() 的坐标是
的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒,问:以
秒,问:以![]() 为顶点的多边形面积是否为定值,若是,请求出此多边形的面积;若不是,请说明理由.
为顶点的多边形面积是否为定值,若是,请求出此多边形的面积;若不是,请说明理由.
(3)如图2,![]() 是线段
是线段![]() 上一点,使
上一点,使![]() ,点
,点![]() 是线段
是线段![]() 上任意一点(
上任意一点(![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)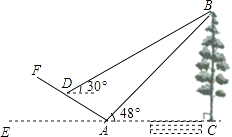
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人玩摸球游戏:一个不透明的袋子中装有相同大小的3个球,球上分别标有数字1,2,3.首先,甲从中随机摸出一个球,然后,乙从剩下的球中随机摸出一个球,比较球上的数字,较大的获胜.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( ) 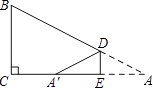
A.![]()
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com