
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)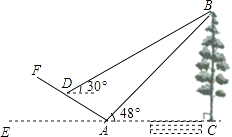
【答案】解:如图,过点D作DG⊥BC于G,DH⊥CE于H, 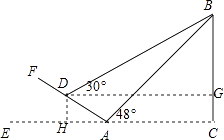
则四边形DHCG为矩形.
故DG=CH,CG=DH,DG∥HC,
∴∠DAH=∠FAE=30°,
在直角三角形AHD中,
∵∠DAH=30°,AD=6,
∴DH=3,AH=3 ![]() ,
,
∴CG=3,
设BC为x,
在直角三角形ABC中,AC= ![]() =
= ![]() ,
,
∴DG=3 ![]() +
+ ![]() ,BG=x﹣3,
,BG=x﹣3,
在直角三角形BDG中,∵BG=DGtan30°,
∴x﹣3=(3 ![]() +
+ ![]() )
) ![]()
解得:x≈13,
∴大树的高度为:13米.
【解析】根据解直角三角形中的实际应用,通过做辅助线,得到四边形DHCG为矩形,在直角三角形AHD中,由∠DAH=30°,AD=6,得到DH=3,AH=3 ![]() ,求出CG=3,在直角三角形ABC中,根据解直角三角形得到AC=
,求出CG=3,在直角三角形ABC中,根据解直角三角形得到AC= ![]() ,得到DG=3
,得到DG=3 ![]() +
+ ![]() ,BG=x﹣3,在直角三角形BDG中,由BG=DGtan30°,求出x的值即可.
,BG=x﹣3,在直角三角形BDG中,由BG=DGtan30°,求出x的值即可.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16
B.14
C.12
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2 400 m,先到终点的人原地休息.已知甲先出发4 min,在整个步行过程中,甲、乙两人的距离y(m)与甲出发的时间t(min)之间的关系如图所示,以下结论:①甲步行的速度为60 m/min;②乙走完全程用了32 min;③乙用16 min追上甲;④乙到达终点时,甲离终点还有300 m,其中正确的结论有______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图∠1=∠2,∠3=∠4,∠5=∠6,∠1=60°,∠7=20°
(1)试说明AC⊥BD
(2)求∠3及∠5的度数
(3)求四边形ABCD各内角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.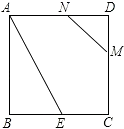
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC边AB的垂直平分线,分别交AB、BC于D、E。AE平分∠BAC. 设∠B = x(单位:度),∠C = y(单位:度).
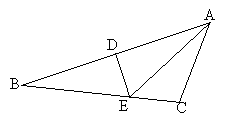
(1)求y随x变化的函数关系式,并写出自变量x的取值范围;
(2)请讨论当△ABC为等腰三角形时,∠B为多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com