
【题目】如图,DE是△ABC边AB的垂直平分线,分别交AB、BC于D、E。AE平分∠BAC. 设∠B = x(单位:度),∠C = y(单位:度).
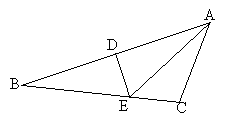
(1)求y随x变化的函数关系式,并写出自变量x的取值范围;
(2)请讨论当△ABC为等腰三角形时,∠B为多少度?
【答案】(1)y = 180 – 3x,0< x <60(2)45或36
【解析】解:(1)∵DE 垂直平分AB,∴∠BAE = ∠B =x,
又∵AE平分∠BAC,∴∠BAC =2∠BAE = 2x---------------------1/
∴ y = 180 – 3x ------------------------------------------2/
0< x <60-----------------------------------------------3/
(2)显然,AC≠BC-----------------------------------------4/.
若 AB = AC,此时,x = y,即:180-3x = x--------------5/
得:x = 45(度);------------------------------------6/
若 AB = BC,此时,2x = y,即:180 – 3x = 2x
得:x = 36(度).
∴当△ABC为等腰三角形时,∠B分别为45或36----------------8/
(1)根据线段的垂直平分线求出∠BAE的度数,求出∠BAC即可;
(2)AB=AC时,得出180-3x=x,求出即可;AB=BC时,得出180-3x=2x,求出即可.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)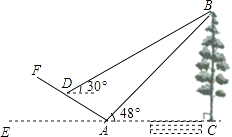
查看答案和解析>>
科目:初中数学 来源: 题型:
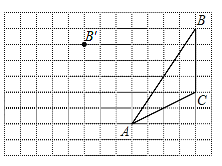
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为 1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B 的对应点 B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)线段 AA′与线段 BB′的数量和位置关系是___________;
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图所示,根据题中相关信息回答下列问题: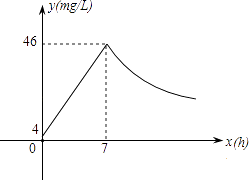
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.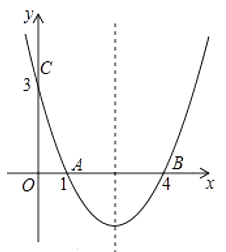
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( ) 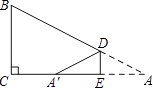
A.![]()
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在![]() ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
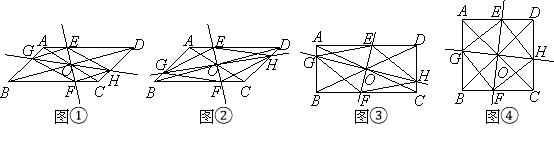
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y= ![]() (x>0)的图象与边BC交与点F.
(x>0)的图象与边BC交与点F.
(1)若△OAE、△OCF的面积分别为S1、S2 , 且S1+S2=2,求k的值;
(2)在(1)的结论下,当OA=2,OC=4时,求三角形OEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2 , 后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求: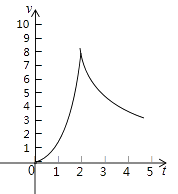
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com