
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2 , 后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求: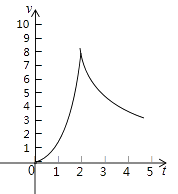
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
【答案】
(1)解:v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v= ![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v= ![]() (2<t≤5)
(2<t≤5)
(2)解:∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分
(3)解:弹珠在第5秒末离开轨道,其速度为v= ![]() =3.2(米/分)
=3.2(米/分)
【解析】(1)根据二次函数的图象过点(1,2),反比例函数的图象经过点(2,8),利用待定系数法可分别求得;
(2)把t=2代入(1)中二次函数的解析式可求得;
(3)把t=5代入(1)中反比例函数的解析式可求得.


科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC边AB的垂直平分线,分别交AB、BC于D、E。AE平分∠BAC. 设∠B = x(单位:度),∠C = y(单位:度).
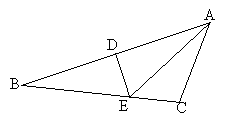
(1)求y随x变化的函数关系式,并写出自变量x的取值范围;
(2)请讨论当△ABC为等腰三角形时,∠B为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B 村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每100km耗油3升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,为满足口罩需求,某商店决定购进A,B两种口罩。若购进A口罩10盒,B口罩5盒,需要1000元。若购进A口罩4盒,B口罩3盒,需要550元.
(1)求A,B两种口罩每盒需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种口罩,考虑到市场需求,要求购进A口罩的数量不少于B口罩数量的6倍,且不超过B口罩数量的8倍,那么该商店共有几种进货方案?
(3)若销售每盒A口罩可以获利润20元,每盒B口罩可以获利润30元,在(2)的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
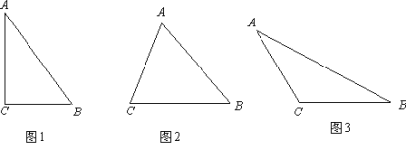
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A′B′C′是△ABC 经过平移得到的,△ABC 中任意一点 P(x1,y1)平移后的对应点为 P′(x1+6,y1﹣5).
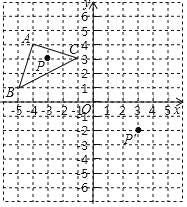
(1)请写出三角形 ABC 平移的过程;
(2)分别写出点 A′,B′,C′的坐标;
(3)画出平移后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com