
【题目】在平面直角坐标系中,过点P(0,a)作直线l分别交![]()
![]() 于点M、N,
于点M、N,
(1)若m=4,MN∥x轴,![]() ,求n的值;
,求n的值;
(2)若a=5,PM=PN,点M的横坐标为3,求m-n的值;
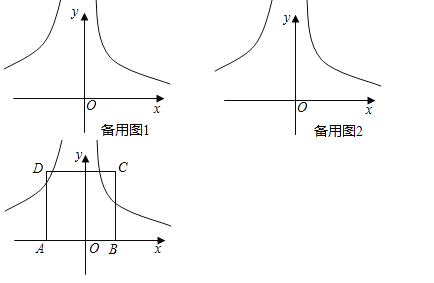
(3)如图,若m=4,n=-6,点A(d,0)为x轴的负半轴上一点,B为x轴上点A右侧一点,AB=4,以AB为一边向上作正方形ABCD,若正方形ABCD与![]()
![]() 都有交点,求d的范围.
都有交点,求d的范围.
【答案】(1)n=-8;(2)30 ;(3)-3≤d≤![]()
【解析】
(1)点P(0,a),则点M、N的坐标分别为(![]() ,a)、(
,a)、(![]() ,a),则S△MON=6=
,a),则S△MON=6=![]() ×MN×OP=
×MN×OP=![]() ×(
×(![]() -
-![]() )×a,即可求解;
)×a,即可求解;
(2)点M、N的坐标分别为(![]() ,a)、(
,a)、(![]() ,a),PM=PN,则
,a),PM=PN,则![]() =-
=-![]() ,解得:m=-n,即可求解;
,解得:m=-n,即可求解;
(3)若正方形ABCD与y=![]() (m>0、x>0),y=
(m>0、x>0),y=![]() (n<0,x<0)都有交点,则HD≥0且CG≥0,即可求解.
(n<0,x<0)都有交点,则HD≥0且CG≥0,即可求解.
解:(1)点P(0,a),则点M、N的坐标分别为(![]() ,a)、(
,a)、(![]() ,a),
,a),
则S△MON=6=![]() ×MN×OP=
×MN×OP=![]() ×(
×(![]() -
-![]() )×a
)×a
解得:n=-8;
(2)点M、N的坐标分别为(![]() ,a)、(
,a)、(![]() ,a),
,a),
∵PM=PN,则![]() =-
=-![]() ,解得:m=-n,
,解得:m=-n,
若a=5,点M的横坐标为3,则点M(3,5),故m=3×5=15=-n,
故m-n=30;
(3)点A(d,0),则点B(d+4,0),点D、C的坐标分别为(d,4)、(d+4,4),
设正方形交两个反比例函数于点G、H,则点G、H的坐标分别为(d,-![]() )、(d+4,
)、(d+4,![]() ),
),
若正方形ABCD与y=![]() (m>0、x>0),y=
(m>0、x>0),y=![]() (n<0,x<0)都有交点,
(n<0,x<0)都有交点,
则HD≥0且CG≥0,即
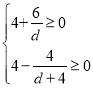 ,且d<0,d+4>0,
,且d<0,d+4>0,
解得:-3≤d≤![]() ,
,
故d的范围为:-3≤d≤![]() .
.


科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.
的图象相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.
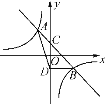
(1)求一次函数与反比例函数的表达式;
(2)若点D与点C关于x轴对称,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(性质探究)
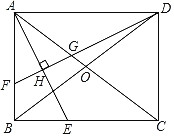
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
(1)判断△AFG的形状并说明理由.
(2)求证:BF=2OG.
(迁移应用)
(3)记△DGO的面积为S1,△DBF的面积为S2,当![]() 时,求
时,求![]() 的值.
的值.
(拓展延伸)
(4)若DF交射线AB于点F,(性质探究)中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的![]() 时,请直接写出tan∠BAE的值.
时,请直接写出tan∠BAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=
x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=![]() x2+bx+c经过点B,C,与x轴的另一个交点为点A.
x2+bx+c经过点B,C,与x轴的另一个交点为点A.
(1)求抛物线的解析式;
(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;
(3)若点M是抛物线上一点,请直接写出使∠MBC=![]() ∠ABC的点M的坐标.
∠ABC的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
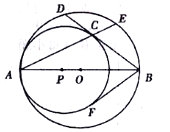
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 是半径
是半径![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),
重合),![]() 为⊙
为⊙![]() 的半径,⊙
的半径,⊙![]() 的弦
的弦![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() .
.
(1)设![]() ,则
,则![]() 与
与![]() 之间的数量关系是什么?请说明理由.
之间的数量关系是什么?请说明理由.
(2)若![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,点
时,点![]() 是弦
是弦![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |

根据统计图表中的信息,解答下列问题:
(1)本次调查的学生总人数为 ;
(2)补全条形统计图;
(3)将调查结果绘成扇形统计图,则“音乐舞蹈”社团所在扇形所对应的圆心角为 ;
(4)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的二次函数![]() (k为常数)和一次函数
(k为常数)和一次函数![]() .
.
(1)求证:函数![]() 的图象与x轴有交点.
的图象与x轴有交点.
(2)已知函数![]() 的图象与x轴的两个交点间的距离等于3,
的图象与x轴的两个交点间的距离等于3,
①试求此时k的值.
②若![]() ,试求x的取值范围.
,试求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
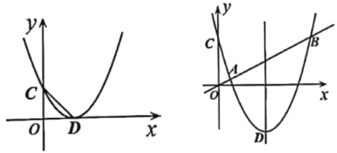
【题目】已知:二次函数y=x2-2mx-m2+4m-2的对称轴为l,抛物线与y轴交于点C,顶点为D.
(1)判断抛物线与x轴的交点情况;
(2)如图1,当m=1时,点P为第一象限内抛物线上一点,且△PCD是以PD为腰的等腰三角形,求点P的坐标;
(3)如图2,直线![]() 和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,
和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,![]() 时,求h的最大值.
时,求h的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com