
����Ŀ��������̽����
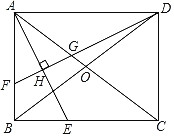
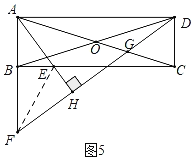
��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AEƽ�֡�BAC����BC�ڵ�E����DF��AE�ڵ�H���ֱ�AB��AC�ڵ�F��G��
��1���жϡ�AFG����״��˵�����ɣ�
��2����֤��BF=2OG��
��Ǩ��Ӧ�ã�
��3���ǡ�DGO�����ΪS1����DBF�����ΪS2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
����չ���죩
��4����DF������AB�ڵ�F��������̽�����е������������䣬����EF������BEF�����Ϊ����ABCD�����![]() ʱ����ֱ��д��tan��BAE��ֵ��
ʱ����ֱ��д��tan��BAE��ֵ��
���𰸡���1�����������Σ����ɼ���������2������������3��![]() ����4��
����4��![]() ��
��![]()
��������
��1����ͼ1�У���AFG�ǵ��������Σ�����ȫ�������ε�����֤�����ɣ�
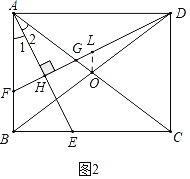
��2����ͼ2�У�����O��OL��AB��DF��L�����AFG=��OLG������֤��OG=OL����֤��BF=2OL���ɽ�����⣮
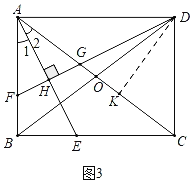
��3����ͼ3�У�����D��DK��AC��K�����DKA=��CDA=90�����������������ε����ʽ�����⼴�ɣ�
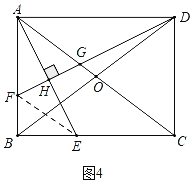
��4����OG=a��AG=k�����������Σ�����ͼ4�У�����EF������F���߶�AB��ʱ����G��OA�ϣ�����ͼ5�У�����F��AB���ӳ�����ʱ����G���߶�OC�ϣ�����EF���ֱ���⼴�ɽ�����⣮
��1���⣺��ͼ1�У���AFG�ǵ��������Σ�

���ɣ���AEƽ�֡�BAC��
���1=��2��
��DF��AE��
���AHF=��AHG=90����
��AH=AH��
���AHF�ա�AHG��ASA����
��AF=AG��
���AFG�ǵ��������Σ�
��2��֤������ͼ2�У�����O��OL��AB��DF��L�����AFG=��OLG��
��AF=AG��
���AFG=��AGF��
�ߡ�AGF=��OGL��
���OGL=��OLG��
��OG=OL��
��OL��AB��
���DLO�ס�DFB��
��![]() ��
��
���ı���ABCD�Ǿ��Σ�
��BD=2OD��
��BF=2OL��
��BF=2OG��
��3���⣺��ͼ3�У�����D��DK��AC��K�����DKA=��CDA=90����
�ߡ�DAK=��CAD��
���ADK�ס�ACD��
��![]() ��
��
��S1=![]() OGDK��S2=
OGDK��S2=![]() BFAD��
BFAD��
�֡�BF=2OG��![]() ��
��
��![]() ����CD=2x��AC=3x����AD=
����CD=2x��AC=3x����AD= ![]() ��
��
��![]() ��
��
��4���⣺��OG=a��AG=k��
����ͼ4�У�����EF������F���߶�AB��ʱ����G��OA�ϣ�
��AF=AG��BF=2OG��
��AF=AG=k��BF=2a��
��AB=k+2a��AC=2��k+a����
��AD2=AC2��CD2=[2��k+a��]2����k+2a��2=3k2+4ka��
�ߡ�ABE=��DAF=90������BAE=��ADF��
���ABE�ס�DAF��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�����⣺![]() =AD��k+2a����
=AD��k+2a����
��AD2=10ka��
��10ka=3k2+4ka��
��k=2a��
��AD= ![]() ��
��
��BE= ![]() =
= ![]() ��AB=4a��
��AB=4a��
��tan��BAE= ![]() ��
��
����ͼ5�У�����F��AB���ӳ�����ʱ����G���߶�OC�ϣ�����EF��
��AF=AG��BF=2OG��
��AF=AG=k��BF=2a��
��AB=k��2a��AC=2��k��a����
��AD2=AC2��CD2=[2��k��a��]2����k��2a��2=3k2��4ka��
�ߡ�ABE=��DAF=90������BAE=��ADF��
���ABE�ס�DAF��
��![]() ��
��
��![]() ��
��
�� ![]() ��
��
�����⣺![]() =AD/span>��k��2a����
=AD/span>��k��2a����
��AD2=10ka��
��10ka=3k2��4ka��
��k= ![]() ��
��
��AD= ![]() ��
��
��![]() ��AB=
��AB= ![]() ��
��
��tan��BAE= ![]() ��
��
����������tan��BAE��ֵΪ![]() ��
��![]() ��
��


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
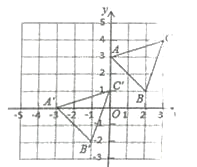
����Ŀ����ͼ��������A��B��C����������ABC����ij��ƽ�Ƶõ��ģ���A���A������B���B������C���C���ֱ��Ӧ���۲���������֮��Ĺ�ϵ������������⣮
(1)�ֱ�д����A����B����C����A������B������C�������꣬��˵��������A��B��C����������ABC����������ƽ�Ƶõ��ģ�
(2)����M (a+2�� 4-b)�ǵ�N (2a-3�� 2b- 5)ͨ��(1)�еı任�õ��ģ���a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
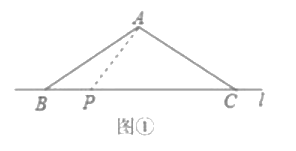
����Ŀ����ѧ��Ȥ����ϣ�С�½�����![]() �ĵױ�
�ĵױ�![]() ��ֱ��
��ֱ��![]() �غϣ�
�غϣ�
��1����ͼ![]() ����
����![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() ���ڵ�ֱ��
���ڵ�ֱ��![]() ���ƶ������ݡ�ֱ����һ�㵽ֱ�������е�������д��߶���̡���С�·���
���ƶ������ݡ�ֱ����һ�㵽ֱ�������е�������д��߶���̡���С�·���![]() ����Сֵ��____________��
����Сֵ��____________��
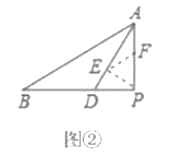
��2��Ϊ��һ�����øý��ۣ��ڣ�1���������£�С�·��֣���![]() ���ʱ����ͼ
���ʱ����ͼ![]() ����
����![]() ����
�У���![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() С�³���̽��
С�³���̽��![]() ����Сֵ��С����
����Сֵ��С����![]() �Ͻ�ȡ
�Ͻ�ȡ![]() ʹ��
ʹ��![]() ����
����![]() ��֤
��֤![]() ���Ӷ���
���Ӷ���![]() ת��Ϊ
ת��Ϊ![]() ת������1�����������
ת������1�����������![]() ����СֵΪ����������
����СֵΪ����������
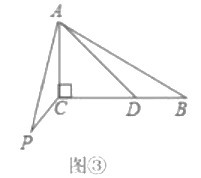
��3��������⣺��ͼ![]() ����
����![]() ��
��![]() ����
����![]() �DZ�
�DZ�![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ���߶�
���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ���õ��߶�
���õ��߶�![]() ����
����![]() �����߶�
�����߶�![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���B=90�㣬��A=60�㣬AC=2![]() +4����M��N�ֱ����߶�AC��AB�ϣ�����ANM��ֱ��MN�۵���ʹ��A�Ķ�Ӧ��Dǡ�������߶�BC�ϣ�����DCMΪֱ��������ʱ���ۺ�MN�ij�Ϊ__��
+4����M��N�ֱ����߶�AC��AB�ϣ�����ANM��ֱ��MN�۵���ʹ��A�Ķ�Ӧ��Dǡ�������߶�BC�ϣ�����DCMΪֱ��������ʱ���ۺ�MN�ij�Ϊ__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
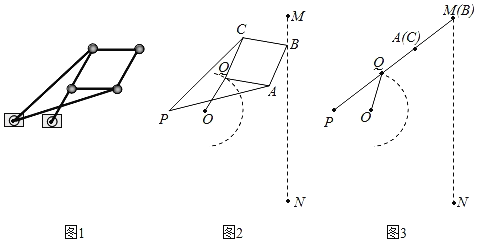
����Ŀ��ͼ1�����߸��������Ӷ��ɵĻ�еװ�ã�ͼ2����ʾ��ͼ����֪O��P����̶�������PA=PC=140cm��AB=BC=CQ=QA=60cm��OQ=50cm��O��P��������OQ������ȣ���OQ�Ƶ�Oת��ʱ����A��B��C��λ����֮�ı䣬��Bǡ�����߶�MN�������˶�������B�˶�����M��Nʱ����A��C�غϣ���P��Q��A��B��ͬһֱ���ϣ���ͼ3����
��1����P��MN�ľ���Ϊ_____cm��
��2������P��O��A��ͬһֱ����ʱ����Q��MN�ľ���Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������������ֽ�ȫ��Ϊ�Ĵ����ֵ������������ʴ���ɼ�������������ʳƷ��320���������ʳƷ��80����
��1��������ɼ��������ʳƷ�����ټ���
��2���ּƻ����üס������ֻ�����8����һ���������������ʳƷȫ���������ֵ�������֪���ֻ��������װ����40����ʳƷ10�������ֻ�������װ�����ʳƷ��20�����������ְ��żס������ֻ���ʱ�м��ַ��������������Ƴ�����
��3���ڵڣ�2���ʵ������£�������ֻ���ÿ�����������4000Ԫ�����ֻ���ÿ�����������3600Ԫ��������Ӧѡ�����ַ�����ʹ��������٣�����������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����P(0��a)��ֱ��l�ֱ�![]()
![]() �ڵ�M��N��
�ڵ�M��N��
��1����m=4��MN��x�ᣬ![]() ����n��ֵ��
����n��ֵ��
��2����a=5��PM=PN����M�ĺ�����Ϊ3����m-n��ֵ��
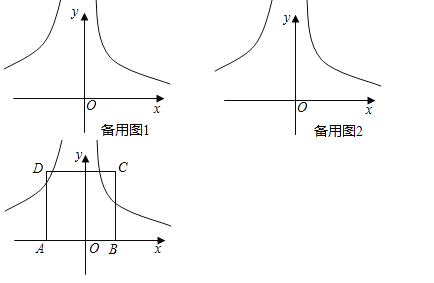
��3����ͼ����m=4��n=-6����A(d,0)Ϊx��ĸ�������һ�㣬BΪx���ϵ�A�Ҳ�һ�㣬AB=4����ABΪһ��������������ABCD����������ABCD��![]()
![]() ���н��㣬��d�ķ�Χ��
���н��㣬��d�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�����![]() �ͺ���
�ͺ���![]() (m�dz�������
(m�dz�������![]() )��ͼ�������( )
)��ͼ�������( )
A. 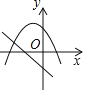 B.
B. 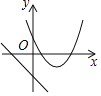
C. 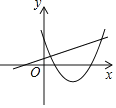 D.
D. 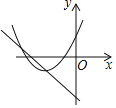
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������٣�ij�������ڳ��ҹ���![]() ��
��![]() ����ů�ֱ���
����ů�ֱ���![]() ���������ۣ�������
���������ۣ�������![]() ��ů�ֱ�
��ů�ֱ�![]() ����
����![]() ��ů�ֱ�
��ů�ֱ�![]() ������Ҫ
������Ҫ![]() Ԫ��������
Ԫ��������![]() ��ů�ֱ�
��ů�ֱ�![]() ����
����![]() ��ů�ֱ�
��ů�ֱ�![]() ��������Ҫ
��������Ҫ![]() Ԫ
Ԫ
��1������![]() ��
��![]() ����ů�ֱ�ÿ���������Ԫ��
����ů�ֱ�ÿ���������Ԫ��
��2���������ʽ����ƣ����ڹ���������ů�ֱ����ʽ��ܳ���![]() Ԫ���蹺��
Ԫ���蹺��![]() ��ů�ֱ�
��ů�ֱ�![]() ������
������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���ڢٵ������£�����![]() ��ů�ֱ���������
��ů�ֱ���������![]() ���������ļ��ֹ�����
���������ļ��ֹ�����
��3���������һ��![]() ��ů�ֱ��˷�Ϊ
��ů�ֱ��˷�Ϊ![]() Ԫ��һ��
Ԫ��һ��![]() ��ů�ֱ��˷�Ϊ
��ů�ֱ��˷�Ϊ![]() Ԫ���ڵ�
Ԫ���ڵ�![]() �ʵĸ��ֹ����У�����
�ʵĸ��ֹ����У�����![]() ��ů�ֱ�����һ�ֹ����������˷����٣������˷��Ƕ���Ԫ��
��ů�ֱ�����һ�ֹ����������˷����٣������˷��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com