
分析 根据完全平方公式,把要求的式子平方,然后利用整体代入即可.
解答 解:∵1<x<2,
∴x-1>0.
∵x+$\frac{1}{x-1}$=19,
∴x-1+$\frac{1}{x-1}$=18,
∵($\sqrt{x-1}$-$\frac{1}{\sqrt{x-1}}$)2=x-1-2+$\frac{1}{x-1}$=16,
∴$\sqrt{x-1}$-$\frac{1}{\sqrt{x-1}}$=±4,
∵1<x<2,
∴$\sqrt{x-1}$>$\frac{1}{\sqrt{x-1}}$
∴$\sqrt{x-1}-\frac{1}{\sqrt{x-1}}$=4.
故答案为4.
点评 本题考查二次根式的化简求值,解题的关键是利用完全平方公式先平方再开方求值,体现了整体代入的解题思想,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 一组数据:4、1、3、1、2的中位数是3 | |
| B. | 了解一批节能灯的使用寿命,适合用普查的方式 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 甲、乙两人在相同条件下各射击20次,他们的成绩平均数相同,方差分别是S甲2=0.4.S乙2=0.6,则甲的射击成绩较稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 口罩种类 | 高档 | 中档 | 低挡 |
| 每人可加工口罩的数量(个) | 160 | 120 | 100 |
| 每个口罩获利(元) | a | b | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
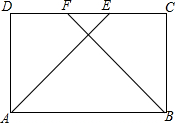 四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.
四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )
如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )| A. | △ABC绕着点A顺时针旋转90°,再向右平移7格 | |
| B. | △ABC向右平移4格,再向上平移7格 | |
| C. | △ABC绕着点A逆时针旋转90°,再向右平移7格 | |
| D. | △ABC向右平移4格,再绕着点B逆时针旋转90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com