
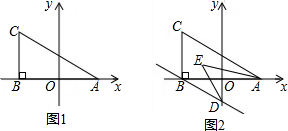
分析 (1)根据非负数的性质求出a、b,得A、B、C坐标即可解决问题.
(2)延长EO到M,利用三角形的外角的性质进行计算即可.
(3)根据同底等高三角形面积相等,先找到点D满足条件,再根据对称性求出另一个点P坐标.
解答 解:(1)∵(a-3)2+$\sqrt{b+3}$=0,
又∵(a-3)2≥0,$\sqrt{b+3}$≥0,
∴a=3,b=-3,
∴点A坐标(3,0),点B坐标(-3,0),点C坐标(-3,2),
∴S△ABC=$\frac{1}{2}$×6×2=6.
(2)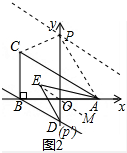 如图2中,延长EO到M,
如图2中,延长EO到M,
∵BD∥AC,
∴∠CAB=∠ABD,
∵∠MOD=∠OED+∠ODE,∠MOA=∠OEA+∠OAE,
∴∠MOD+∠MOA=∠OED+∠OEA+∠OAE+∠ODE,
∴∠AED+$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠BDO=90°,
∴∠AED=90°-$\frac{1}{2}$(∠OBD+∠BDO)=45°.
(3)∵直线AC解析式为y=-$\frac{1}{3}$x+1,
∵BD∥AC,
∴直线BD解析式为y=-$\frac{1}{3}$x-1,
∴点D坐标(0,-1),
∵BD∥AC,
∴S△ABC=S△ACD,
∴P′与D重合,
∴点P′的坐标(0,-1),根据对称性得到P(0,3)也满足条件,
∴点P坐标为(0,-1)或(0,3).
故答案为(0,-1)或(0,3).
点评 本题考查坐标与图形的性质、平行线的性质、三角形的面积等知识,解决问题的关键是平行线间的距离相等,等积问题要想到平行线的这个性质,属于中考常考题型.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a=2,b=-1 | B. | a=-4,b=3 | C. | a=1,b=-7 | D. | a=-7,b=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.
如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 内角和与外角和相等的多边形是四边形 | |
| B. | 十边形的内角和为1440° | |
| C. | 多边形的内角中最多有四个直角 | |
| D. | 十边形共有40条对角线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
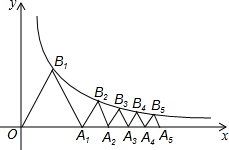 如图,点A1、A2、A3、A4、A5、…、A2015在x轴的正半轴上,点B1、B2、B3、B4、B5、…、B2015在双曲线y=$\frac{\sqrt{3}}{x}$上,若△A1B1O、△A2B2A1、△A3B3A2、△A4B4A3、△A5B5A4、…、△A2015B2015A2014均为等边三角形,求△A2015B2015A2014的边长.
如图,点A1、A2、A3、A4、A5、…、A2015在x轴的正半轴上,点B1、B2、B3、B4、B5、…、B2015在双曲线y=$\frac{\sqrt{3}}{x}$上,若△A1B1O、△A2B2A1、△A3B3A2、△A4B4A3、△A5B5A4、…、△A2015B2015A2014均为等边三角形,求△A2015B2015A2014的边长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com