
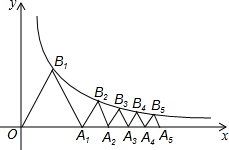
 如图,点A1、A2、A3、A4、A5、…、A2015在x轴的正半轴上,点B1、B2、B3、B4、B5、…、B2015在双曲线y=$\frac{\sqrt{3}}{x}$上,若△A1B1O、△A2B2A1、△A3B3A2、△A4B4A3、△A5B5A4、…、△A2015B2015A2014均为等边三角形,求△A2015B2015A2014的边长.
如图,点A1、A2、A3、A4、A5、…、A2015在x轴的正半轴上,点B1、B2、B3、B4、B5、…、B2015在双曲线y=$\frac{\sqrt{3}}{x}$上,若△A1B1O、△A2B2A1、△A3B3A2、△A4B4A3、△A5B5A4、…、△A2015B2015A2014均为等边三角形,求△A2015B2015A2014的边长. 分析 先求出OA1、OA2、OA3,探究规律归纳得出OAn即可解决问题.
解答 解:设等边三角形△OB1A1的边长为a,则B1坐标为($\frac{a}{2}$,$\frac{\sqrt{3}}{2}$a),
∵B1在反比例函数图象上,
∴$\frac{a}{2}$•$\frac{\sqrt{3}}{2}$a=$\sqrt{3}$,
∴a2=4,
∵a>0,
∴a=2,
∴OA1=2,设等边三角形△A1B2A2的边长为b,则B2(2+$\frac{b}{2}$,$\frac{\sqrt{3}}{2}b$),
∴(2+$\frac{b}{2}$)•$\frac{\sqrt{3}}{2}$b=$\sqrt{3}$,
解得b=2$\sqrt{2}$-2,OA2=2$\sqrt{2}$,设等边三角形△A2B3A3的边长为c,在则B3(2$\sqrt{2}$+$\frac{c}{2}$,$\frac{\sqrt{3}}{2}c$),
∴(2$\sqrt{2}$+$\frac{c}{2}$)•$\frac{\sqrt{3}}{2}$c=$\sqrt{3}$,
解得c=2$\sqrt{3}$-2$\sqrt{2}$,
∴OA3=2$\sqrt{3}$
综上所述:OA1=2,OA2=2$\sqrt{2}$,OA3=2$\sqrt{3}$…OAn=2$\sqrt{n}$,
则△A2015B2015A2014的边长为2$\sqrt{2015}$-2$\sqrt{2014}$.
点评 本题考查反比例函数的有关知识、等边三角形的性质、解题的关键是从一般到特殊探究规律后解决问题,属于中考常考题型.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com