
| ������ | �ǵ���֪�� | $\frac{a}{b}$ | $\frac{b+c}{a}$ |
| ͼ2 | ��A=2��B=90�� | $\sqrt{2}$ | $\sqrt{2}$ |
| ͼ3 | ��A=2��B=60�� | $\sqrt{3}$ | $\sqrt{3}$ |
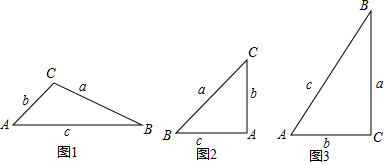
���� ��1��ͼ2�������Σ���Ȼ�ǵ���ֱ�������Σ�����б��cΪ2����ôa=b=$\sqrt{2}$��������õ�ֵ��ͼ3�Ľⷨͬ�ϣ�
��2���ɣ�1���Ľ��ۣ��ɲ²�a��b��c�ĵ�����ϵӦ����$\frac{a}{b}=\frac{b+c}{a}$����ͨ������������������֤�����ӳ�CA��D���ǵ�AD=AB����ô��CAB=2��A=2��CBA���ټ��Ϲ����ǡ�C������֤�á�CBD�ס�CAB���ɴ˵õ�����Ľ��ۣ�
��3��������������ݣ�2���Ľ���ֱ�Ӽ��㼴�ɣ�
��� �⣺��1����ͼ2
�ߡ�A=2��B=90�㣬
���B=45�㣬
���C=45�㣬
��a=$\sqrt{2}$b=$\sqrt{2}$c��
��$\frac{a}{b}=\sqrt{2}$��$\frac{b+c}{a}=\frac{\frac{\sqrt{2}}{2}a+\frac{\sqrt{2}}{2}a}{a}$=$\sqrt{2}$��
��ͼ3���ߡ�A=2��B=60�㣬
���B=30�㣬
���C=90�㣬
��b=$\frac{1}{2}$c��a=$\frac{\sqrt{3}}{2}$c��
��$\frac{a}{b}=\frac{\frac{\sqrt{3}}{2}c}{\frac{1}{2}c}$=$\sqrt{3}$��$\frac{b+c}{a}=\frac{\frac{1}{2}c+c}{\frac{\sqrt{3}}{2}c}$=$\sqrt{3}$��
�ʴ�Ϊ��$\sqrt{2}$��$\sqrt{2}$��$\sqrt{3}$��$\sqrt{3}$��
��2���²⣺$\frac{a}{b}=\frac{b+c}{a}$��
���ɣ���ͼ1��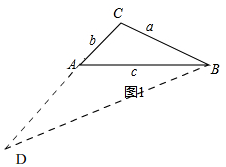
�ӳ�CA��D��ʹAD=AB��
��AD=AB�����D=��ABD��
���CAB=��D+��ABD=2��D��
�ߡ�CAB=2��CBA��
���D=��CBA��
�֡ߡ�C=��C��
���CBD�ס�CAB��
��$\frac{CB}{CA}=\frac{CD}{BC}$��
��$\frac{a}{b}=\frac{b+c}{a}$��
��3���ߡ�ABC�ǵ��������Σ��������A�Ƕ��ǣ����B=��C�ǵǣ�
�ߡ�ABCǡΪһ�����������Σ�
���A=2��B���B=2��A��
�ٵ���A=2��Bʱ��
���A=90�㣬��B=��C=45�㣬
��AB=6ʱ����AC=AB=6��BC=6$\sqrt{2}$��
���ABC���ܳ�Ϊ12+6$\sqrt{2}$��
��CB=6ʱ����AB=AC=3$\sqrt{2}$��
���ABC���ܳ�Ϊ6+6$\sqrt{2}$��
�ڵ���B=2��Aʱ�����������ε��ڽǺ͵ã���A=36�㣬��B=��C=72�㣬
��AB=6ʱ����AB=AC=6��
���ɣ�2��֪��BC=-3+3$\sqrt{5}$��
���ABC���ܳ�Ϊ9+3$\sqrt{5}$��
��BC=6ʱ��
���ɣ�2��֪��AB=AC=3+3$\sqrt{5}$��
���ABC���ܳ�Ϊ12+6$\sqrt{5}$��
������ABC���ܳ�Ϊ12+6$\sqrt{2}$��6+6$\sqrt{2}$��9+3$\sqrt{5}$��12+6$\sqrt{5}$��
���� �������������ۺ��⣬��Ҫ�����˵���ֱ�������ε����ʣ���30���ֱ�������ε����ʣ����������ε��ж������ʣ��������������ε����ʵó���2���Ľ����ǽⱾ��Ĺؼ���Ҫע����ǣ�3���������϶࣬һ��Ҫ�������ۣ���Ҫ©�⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
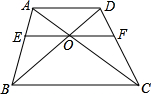 ��ͼ���ı���ABCD�У�AD��BC���Խ����ཻ��O�㣬EF��O�㣬��EF��AD����ͼ��һ����5�����������Σ�
��ͼ���ı���ABCD�У�AD��BC���Խ����ཻ��O�㣬EF��O�㣬��EF��AD����ͼ��һ����5�����������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ����̫���еڶ�ѧ�ڳ�һ����ģ����ѧ�Ծ��������棩 ���ͣ�ѡ����
���м�������ȷ���ǣ� ��
A��a2+a3=2a5 B��a2��a3=a5 C��a2��a3=a6 D��a2+a3=a5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
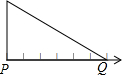 �ۻ��Լ�����һ�������ε�ֽ�壬��������һ�����߸��Ⱦ����С�ڵ㣬ÿ��������С�ڵ�֮��ľ���Ϊ1����λ���ȣ��ְѴ˱߷�����ͼ��ʾ�������ϣ�����P����ʾ������-1.6�����Q����ʾ������4.4��
�ۻ��Լ�����һ�������ε�ֽ�壬��������һ�����߸��Ⱦ����С�ڵ㣬ÿ��������С�ڵ�֮��ľ���Ϊ1����λ���ȣ��ְѴ˱߷�����ͼ��ʾ�������ϣ�����P����ʾ������-1.6�����Q����ʾ������4.4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
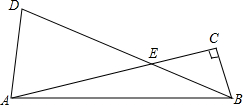 ��Rt��ABC�У���CAB=����б��AB�Ƶ�B˳ʱ����ת2���Ƕȵõ�DB����AC�ڵ�E������AD����AD=kBE��
��Rt��ABC�У���CAB=����б��AB�Ƶ�B˳ʱ����ת2���Ƕȵõ�DB����AC�ڵ�E������AD����AD=kBE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
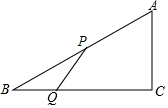 ��ͼ����ֱ��������ABC�У�ֱ�DZ�AC=3cm��BC=4cm����P��Q�ֱ�ΪAB��BC�ϵĶ��㣬�ڵ�P�Ե�A��AB�������B�������ƶ���ͬʱ����Q�Ե�B��BC�������C�������ƶ��������ƶ����ٶȾ�Ϊÿ��1cm����Q�㵽��C��ʱ��P���ֹͣ�ƶ�����P��Q�ƶ���ʱ��t�룮
��ͼ����ֱ��������ABC�У�ֱ�DZ�AC=3cm��BC=4cm����P��Q�ֱ�ΪAB��BC�ϵĶ��㣬�ڵ�P�Ե�A��AB�������B�������ƶ���ͬʱ����Q�Ե�B��BC�������C�������ƶ��������ƶ����ٶȾ�Ϊÿ��1cm����Q�㵽��C��ʱ��P���ֹͣ�ƶ�����P��Q�ƶ���ʱ��t�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
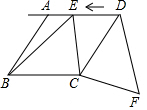 ��ͼ�������߳�Ϊ6�ĵȱ�������ƴ���ı���ABCD����E�ӵ�D��������ÿ��1����λ���ȵ��ٶ���������DA�ķ��������˶������˶�ʱ��Ϊt�룮���߶�CE�Ƶ�C˳ʱ����תһ���Ǧ�����=��BCD�����õ���Ӧ�߶�CF����t=9ʱ��DF�ij�������Сֵ����Сֵ����3$\sqrt{3}$��
��ͼ�������߳�Ϊ6�ĵȱ�������ƴ���ı���ABCD����E�ӵ�D��������ÿ��1����λ���ȵ��ٶ���������DA�ķ��������˶������˶�ʱ��Ϊt�룮���߶�CE�Ƶ�C˳ʱ����תһ���Ǧ�����=��BCD�����õ���Ӧ�߶�CF����t=9ʱ��DF�ij�������Сֵ����Сֵ����3$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | �ȱ������� | C�� | �۽������� | D�� | ֱ�������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com